UM contact 搬运
CONTACT软件基于著名计算力学专家、荷兰代尔夫特理工大学J. J. Kalker教授的三维滚动接触理论(卡尔克理论)开发而成。卡尔克理论最早在文献[14]中提出,而后在文献[17]中详细阐述,文献[19]和[51]分别有一些扩展的描述。Edwin Vollebregt博士在其导师J. J. Kalker教授的基础上,进一步研发和拓展,增加了自动轮轨几何接触分析[49, 50]、考虑第三层介质效应[44, 56]和负斜率特性[53]等功能,采用全新的迭代求解器提高了求解效率[43, 63],现在的程序可称作“Extended CONTACT”。Extended CONTACT是一款用于精细化三维摩擦接触分析的高级仿真软件,主要应用于精确的轮轨蠕滑力特性研究,进而可支持轮轨型面磨耗和滚动接触疲劳分析[24, 25]。
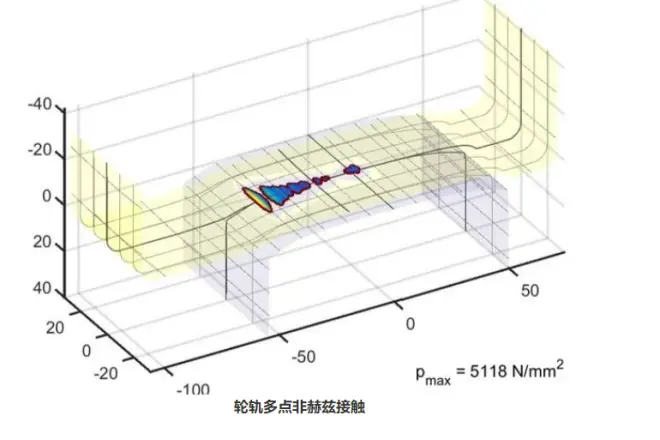
CONTACT的使用方式
CONTACT软件支持以不同的方式运行:
CONTACT Stand-alone version:定义具体的一个或几个关联工况参数,获得完整的计算结果,使用MATLAB绘图子程序进行后处理;
USETAB:求解大量的关联工况,将获得的计算结果制作成数表用于其他商业软件或自编程序;
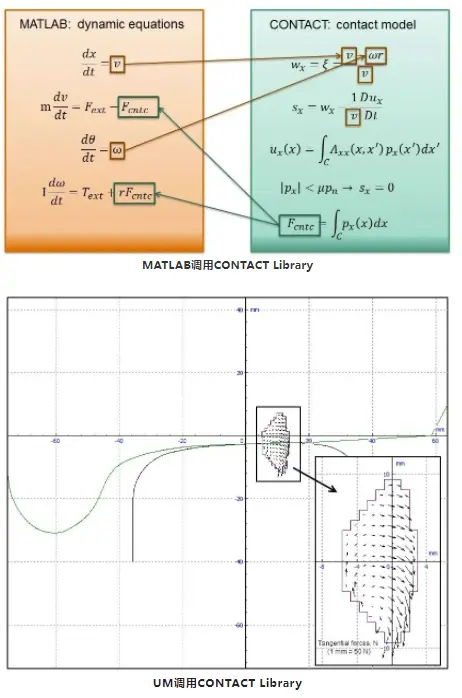
CONTACT Libraries:通过第三方软件以动态链接库(DLL)的形式调用CONTACT的求解内核(完全集成),提供MATLAB、Fortran和C等程序语言接口。
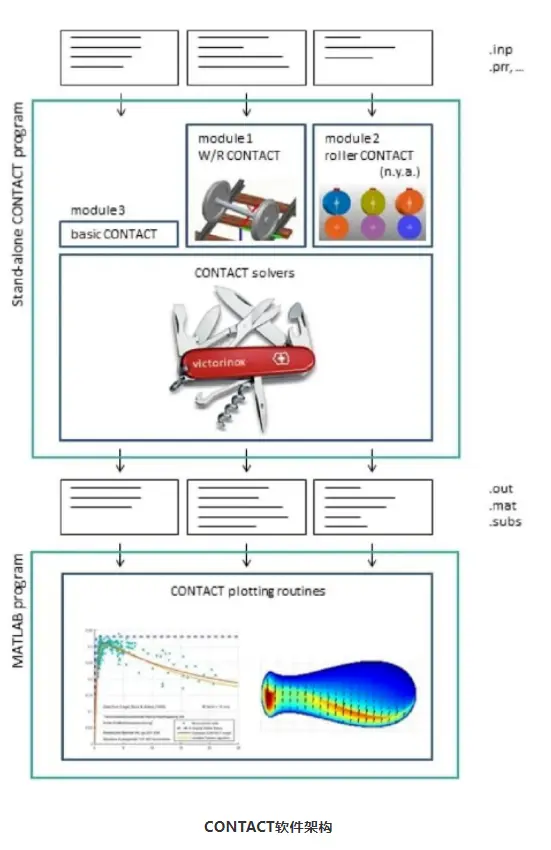
第一种方式是CONTACT软件最基本的运行方式,后面两种方式主要用在车辆系统动力学(VSD)软件的磨耗计算。目前,商业软件Universal Mechanism(完全集成)、GENSYS(完全集成)、NUCARS(数表形式)、SIMPACK Rail[57]与CONTACT已经实现了不同程度的协作。
CONTACT的用户手册
本文内容翻译自用户手册第一章,其他章节主要内容如下:
第二章简略地介绍了接触计算的理论模型,以满足软件操作的最低要求,更详细的内容和参考资料请查阅文献[17, 19, 51];
第三章介绍了软件的基本操作,包括命令行和界面操作、有关模块和工况的术语以及操纵程序的控制符;
第四章介绍轮轨接触分析(一号模块)详细的输入量和输出量;
第五章介绍通用的赫兹和非赫兹接触分析(三号模块)详细的输入量和输出量;
第六章通过一些具体的例子演示CONTACT独立版本的使用方法;
第七章介绍使用MATLAB脚本进行后处理可视化操作;
第八章介绍CONTACT动态链接库的用法;
最后,附录A详细描述了计算输入文件的格式和逻辑选项。
初学者导航
众所周知,CONTACT并不是一个很容易掌握的简单软件。
首先,最主要的原因是完整全面地介绍接触力学的书籍并不多见,虽然Johnson[11]和Kalker[17]的著作非常经典,但要熟悉这些理论和知识本身也是一种挑战,这对数学基础要求很高。作者更推荐Popov[30]的著作,书中对接触现象有更通俗的介绍。此外,文献[55]是关于轮轨蠕滑模型的综述,对于轮轨接触领域的研究人员非常有用。
其次,软件本身要兼容各种各样的工况,这对简单工作流程和简单绘图程序的开发造成了阻碍。
最后,软件至今保留着古老的输入文件结构,其中包含许多控制符和逻辑选项。
其实,在我们看来,如果用户知道接触力学的基本概念和术语,那么操作CONTACT软件并非难事。为了快速熟悉输入文件的内容和格式,建议如下操作:
请将CONTACT用户手册通读一遍,重点(反复)阅读第三、四和五章。
参照用户手册第六章的描述,运行软件自带的算例。
在用户手册第3.3章节和附录A.2放置书签,因为控制符和逻辑选项是需要经常查阅的。
参考文献
R.H. Bentall and K.L. Johnson. Slip in the rolling contact of two dissimilar elastic rollers. Int.J. of Mechanical Sciences, 9:380–404, 1967.
J. Blanco-Lorenzo, J. Santamaria, E.G. Vadillo, and N. Correa. On the influence of conformity on wheel-rail rolling contact mechanics. Tribology International, 103:647–667, 2016.
J. Blanco-Lorenzo, E.A.H. Vollebregt, J. Santamaria, and E.G. Vadillo. Approximating the influence coefficients of non-planar elastic solids for conformal contact analysis. Tribology International, 154:106671, 2021.
A.F. Bower. Applied Mechanics of Solids. CRC Press, Taylor and Francis Group, Boca Raton, 2010. See www.solidmechanics.org.
R.R. Craig Jr. and A.J. Kurdila. Fundamentals of structural dynamics, 2nd edition. John Wiley & Sons, Hoboken, New Jersey, 2006.
B.E. Croft, E.A.H. Vollebregt, and D.J. Thompson. An investigation of velocity-dependent friction in wheel-rail rolling contact. In M. Uchida, T. Maeda, and K. Goto, editors, Proceedings of the 10th International Workshop on Railway Noise, Nagahama, Japan, 2010.
B. Engel, H.P. Beck, and J. Alders. Verschleißreduzierende Radschlupfregelung mit hoher Kraftschlussausnutzung. Elektrische Bahnen, 96:201–209, 1998.
M. Ertz and K. Knothe. A comparison of analytical and numerical methods for the calculation of temperatures in wheel/rail contact. Wear, 253:498–508, 2002.
R.C. Hibbeler. Engineering Mechanics - Statics and Dynamics, 13th Edition. Pearson Prentice Hall, Upper Saddle River, New Jersey, 2012.
K. Hou, J. Kalousek, and E. Magel. Rheological model of solid layer in rolling contact. Wear, 211:134–140, 1997.
K.L. Johnson. Contact Mechanics. Cambridge University Press, Cambridge (UK), 1985.
J.J. Kalker. On the rolling contact of two elastic bodies in the presence of dry friction. PhD thesis, Delft University of Technology, 1967.
J.J. Kalker. Simplified theory of rolling contact. Delft Progress Report Series C1, 1:1–10, 1973.
J.J. Kalker. The computation of three-dimensional rolling contact with dry friction. Int. Journ. for Numerical Methods in Engineering, 14:1293–1307, 1979.
J.J. Kalker. A fast algorithm for the simplified theory of rolling contact. Vehicle System Dynamics, 11:1–13, 1982.
J.J. Kalker. Numerical calculation of the elastic field in a half-space. Comm. Appl. Num. Meth., 2:401–410, 1986. Reprinted as Appendix C in [17].
J.J. Kalker. Three-Dimensional Elastic Bodies in Rolling Contact, volume 2 of Solid Mechanics and its Applications. Kluwer Academic Publishers, Dordrecht, Netherlands, 1990.
J.J. Kalker. Book of tables for the Hertzian creep-force law. In Zobory [64], pages 11–20.
J.J. Kalker. Rolling contact phenomena - linear elasticity. In B. Jacobson and J.J. Kalker, editors, Rolling Contact Phenomena, volume 411 of CISM Courses and Lectures, pages 1–85. Springer-Verlag, Wien New York, 2000.
J.J. Kalker, F.M. Dekking, and E.A.H. Vollebregt. Simulation of rough, elastic contacts. Journal of Applied Mechanics, 64(2):361–368, 1997.
Zili Li. Wheel-rail rolling contact and its application to wear simulation. PhD thesis, Delft University of Technology, 2002.
A.E.H. Love. Stress produced in a semi-infinite solid by pressure on part of the boundary. Philosophical Transactions of the Royal Society of London, A228:377–420, 1929.
M. Malvezzi, E. Meli, S. Falomi, and A. Rindi. Determination of wheel-rail contact points with semianalytic methods. Multibody System Dynamics, 20:327–358, 2008.
S.Z. Meymand, A. Keylin, and M. Ahmadian. A survey of wheel-rail contact models for rail vehicles. Vehicle System Dynamics, 54:368–428, 2016.
R. Munisamy, D.A. Hills, and D. Nowell. Brief note on the tractive rolling of dissimilar elastic cylinders. Int. Journ. of Mechanical Sciences, 33(3):225–228, 1991.
P.M. Naghdi. P.M. Naghdi’s Notes on Continuum Mechanics. University of California, Department of Mechanical Engineering, Berkeley, 2001.
J.B. Nielsen and A. Theiler. Tangential contact problem with friction coefficients depending on sliding velocity. In Zobory [64], pages 44–51.
J. Piotrowski, B.B. Liu, and S. Bruni. The Kalker book of tables for non-Hertzian contact of wheel and rail. Vehicle System Dynamics, 55:875–901, 2017. DOI: 10.1080/00423114.2017.1291980.
O. Polach. Creep forces in simulations of traction vehicles running on adhesion limit. Wear, 258:992–1000, 2005.
V.L. Popov. Contact Mechanics and Friction. Physical Principles and Applications. SpringerVerlag, Berlin, 2010.
D. Roylance. Engineering viscoelasticity. Technical report, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001.
A.A. Shabana. Dynamics of Multibody Systems – Fourth Edition. Cambridge University Press, New York, 2013.
A.A. Shabana, K.E. Zaazaa, and H. Sugiyama. Railroad Vehicle Dynamics: A Computational Approach. CRC Press, Boca Raton, 2008.
P. Shackleton and S.D. Iwnicki. Wheel-rail contact benchmark, version 3.0. Rail Technology Unit, Manchester Metropolitan University, 2006.
P. Shackleton and S.D. Iwnicki. Comparison of wheel-rail contact codes for railway vehicle simulation: an introduction to the Manchester Contact Benchmark and initial results. Vehicle System Dynamics, 46(1-2):129–149, 2008.
M. Spiryagin, O. Polach, and C. Cole. Creep force modelling for rail traction vehicles based on the Fastsim algorithm. Vehicle System Dynamics, 51:1765–1783, 2013.
A.S.K.S. Tjoeng and J.J. Kalker. User’s manual for the program DUVOROL in Algol 60 & Fortran for the computation of three-dimensional rolling contact with dry friction. Technical report, Delft University of Technology, Delft, June 1980.
E.A.H. Vollebregt. A Gauss-Seidel type solver for special convex programs, with application to frictional contact mechanics. J. of Optimization Theory and Applications, 87(1):47–67, 1995.
E.A.H. Vollebregt. Refinement of Kalker’s rolling contact model. In A. Bracciali, editor, Proceedingsofthe8thInternationalConferenceonContactMechanicsandWearofRail/Wheel Systems, pages 149–156, Firenze, Italy, 2009. University of Firenze.
E.A.H. Vollebregt. User guide for CONTACT, J.J. Kalker’s variational contact model. Technical Report TR09-03, v9.1, VORtech, 2009.
E.A.H. Vollebregt. Improving the speed and accuracy of the frictional rolling contact model “CONTACT”. In B.H.V. Topping, J.M. Adam, F.J. Pallarés, R. Bru, and M.L. Romero, editors, Proceedings of the 10th International Conference on Computational Structures Technology, pages 1–15, Stirlingshire, United Kingdom, 2010. Civil-Comp Press. DOI: 10.4203/ccp.93.17.
E.A.H. Vollebregt. The Bound-Constrained Conjugate Gradients method for non-negative matrices. J. of Optimization Theory and Applications, 162(3):931–953, 2014. DOI: 10.1007/s10957-013-0499-x.
E.A.H. Vollebregt. A new solver for the elastic normal contact problem using conjugate gradients, deflation, and an FFT-based preconditioner. J. of Computational Physics, 257, Part A:333–351, 2014.
E.A.H. Vollebregt. Numerical modeling of measured railway creep versus creep-force curves with CONTACT. Wear, 314:87–95, 2014.
E.A.H. Vollebregt. New insights in non-steady rolling contact. In M. Rosenberger, editor, Proceedings of the 24th International Symposium on Dynamics of Vehicles on Roads and Tracks, Graz, Austria, 2015. IAVSD.
E.A.H. Vollebregt. Updates on the rocking phenomenon. In M. Spiryagin, T. Gordon, C. Cole, and T. McSweeney, editors, Proceedings of the 25th International Symposium on Dynamics of Vehicles on Roads and Tracks, pages 605–611, Rockhampton, Queensland, Australia, 2017. IAVSD.
E.A.H. Vollebregt. Comments on “the Kalker book of tables for non-Hertzian contact of wheel and rail”. Vehicle System Dynamics, 56(9):1451–1459, 2018. DOI: 10.1080/00423114.2017.1421767.
E.A.H. Vollebregt. Conformal contact: Corrections and new results. Vehicle System Dynamics, 56(10):1622–1632, 2018. DOI: 10.1080/00423114.2018.1424917.
E.A.H. Vollebregt. Detailed wheel/rail geometry processing using the planar contact approach. Vehicle System Dynamics, 2020. DOI: 10.1080/00423114.2020.1853180, open access.
E.A.H. Vollebregt. Detailed wheel/rail geometry processing using the conformal contact approach. Multibody System Dynamics, 52:135–167, 2021. Open access.
E.A.H. Vollebregt, S.D. Iwnicki, G. Xie, and P. Shackleton. Assessing the accuracy of different simplified frictional rolling contact algorithms. Vehicle System Dynamics, 50(1):1–17, 2012. DOI: 10.1080/00423114.2011.552618.
E.A.H. Vollebregt, J.J. Kalker, and G.Q. Wang. CONTACT’93 users manual. Technical report, Delft University of Technology, 1993.
E.A.H.VollebregtandH.M.Schuttelaars. Quasi-staticanalysisof2-dimensionalrollingcontact with slip-velocity dependent friction. J. of Sound and Vibration, 331(9):2141–2155, 2012. DOI: 10.1016/j.jsv.2012.01.011.
E.A.H.VollebregtandA.Segal. Solvingconformalwheel-railrollingcontactproblems. Vehicle System Dynamics, 52(suppl. 1):455–468, 2014. DOI: 10.1080/00423114.2014.906634.
E.A.H. Vollebregt, K. Six, and O. Polach. Challenges and progress in the understanding and modelling of the wheel–rail creep forces. Vehicle System Dynamics, 59(7):1026–1068, 2021.
E.A.H. Vollebregt and C.D. van der Wekken. Advanced modeling of wheel-rail friction phenomena. Technical Report TR19-11, VORtech, November 2019. FRA project.
E.A.H. Vollebregt, C. Weidemann, and A. Kienberger. Use of “CONTACT” in multi-body vehicle dynamics and profile wear simulation: Initial results. In S.D. Iwnicki, editor, Proceedings of the 22nd International Symposium on Dynamics of Vehicles on Roads and Tracks, pages 1–6, Manchester, 2011. IAVSD.
E.A.H.VollebregtandP.Wilders. FASTSIM2: asecondorderaccuratefrictionalrollingcontact algorithm. Comput.Mech., 47(1):105–116, 2010. DOI: 10.1007/s00466-010-0536-7, open access.
G. Wang and J.J. Kalker. Three-dimensional rolling contact of two viscoelastic bodies. In A. Curnier, editor, Contact Mechanics. Proceedings; International Symposium, October 7 - 9, 1992, Ecole Polytechnique Fédérale de Lausanne, pages 477–490, Lausanne, 1992. Presses Polytechniques et Universitaires Romandes.
G. Wang and K. Knothe. Stress analysis for rolling contact between two viscoelastic cylinders. Journal of Applied Mechanics; Transactions ASME, 60:310–317, 1993.
C.D. van der Wekken and E.A.H. Vollebregt. Numerical calculation of the elastic field in a half-space using bilinear elements. Mathematics and Mechanics of Solids, 24(11):3537–3553, 2019.
C.D. van der Wekken, E.A.H. Vollebregt, and C. Vuik. Occurrence and removal of wiggles in transient rolling contact simulation. In J. Ambrósio, W. Schielen, and J. Pombo, editors, Proceedings of EuroMech colloquim 578 on Rolling Contact Mechanics for Multibody System Dynamics, pages 1–11, Lisbon, Portugal, 2017. IDMEC.
J. Zhao, E.A.H. Vollebregt, and C.W. Oosterlee. A fast nonlinear conjugate gradient based method for 3D concentrated frictional contact problems. J. of Computational Physics, 288:86– 100, 2015.
I. Zobory, editor. Proceedings of the 2nd Mini Conference on Contact mechanics and Wear of Wheel/Rail systems. Technical University of Budapest, Hungary, 1996.

