【超难数独】灯塔数独

2023-02-19 02:29 作者:黑羽夜风 0人读过 | 我要投稿

题目介绍

这是一道分享在CTC上的特殊数独，作者是来自德国“臭名昭著”的数独大佬 Phistomefel

原题链接：https://app.crackingthecryptic.com/sudoku/fLtm97H9GD

下面我先把题目规则翻译一下，

规则1：整个数独表格为9*9大小，一共81个单元格，包含9个不规则区域，从1到9的每一个数字必须出现在每一行、每一列和每一区域。
规则2：每个区域都是一个由九个相连的单元格组成的集合，每个区域不一定是3*3的正方形，可能是任意形状。区域和区域之间有边界。(参考“锯齿数独”）
规则3：带圈的数字（即“灯塔”）表示它这个单元格所在行和列中的区域边界数之和，同时这个数也符合规则1。
规则4：每个区域需要自行确定边界。整个数独表格的外缘不计算在边界数中。

下面是一个符合灯塔规则的例子：

例图来源：https://www.bilibili.com/opus/763136657009410104?spm_id_from=333.999.0.0

喜欢挑战的数独爱好者可以先自行做题，想直接看结果的可以跳到最后。

下面黑羽我分享一下我的解题过程：

（分割线防止剧透）

解题思路

先把数独进行一个行列标注，方便描述

逻辑起点：观察整个图发现，只有A1有带圈数字，所以先看A1

A1是圈9，说明：

左上角A1能看到所有9个区域，这样的话包含A1的区域必须被另一个区域包住，以下称“包裹区”（不然会分出10个区域）
且必占用2条被看见的边界(含A1区和包裹区两个区域的边界）
剩下所有区域必须与左边框相接或者与上边框相接，（不然无法被A1看见）
包含右下角J9的区域只能是1*9或者9*1的长条形（理由同上）
包含右下角J8 H9的区域也得是长度8或9的长条形（理由同上）
包含右下角H8的区域必须为长度等于8的长条形加上G列或7行的其中1块（理由同上）

2.C1有圈，且比9小（同一行数字最大为9,且已经有A1=9），说明：

包含A1的区域不会占据C列（不然C1的灯塔数会大于等于9，不满足A1>C1）
C1处在包裹区内，且是8（必能看到除含A1区外的其他所有区，少看1条含A1区的横向边）

3.要同时满足1和2两个推论，则含有A1的区域只有两种可能：

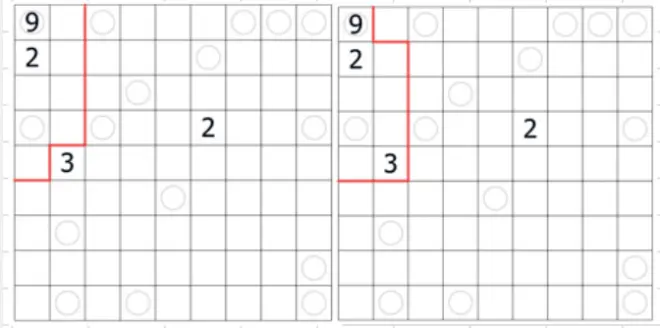
4要同时满足1和2和3，则包裹区（黄色区域）必须包含以下几个单元格：

5.综合1，2，4数据可得下图：

6.接着观察A4和C4,因为A4与A1在同一列，C4和C1同一列，所以A4<A1=9，C4<C1=8,C4=A4-1, 且A4和A1共区域，C1和C4共区域，所以可知必存在一个区域只在前三行出现，又因为A列至多有4条边界，所以第1行必须有至少5条边界，所以下述两种情况均不可能，占第一行其中4格的情况与第一种情况类似，所以不再列出。所以只能是占第一行的其中三格，所以是3*3的正方形，但正方形区域的位置暂时无法确定。