（合计1486字，用时120min——）

身体不舒服，断断续续地整理的，高等数学的定义是比较多，比较简单的，为了踏实还是全部耐着性子整理一遍，区别就是，难一点的内容以后再花时间反复，简单的内容，重复的概率就不太大了。数学放了太久，需要温习。

第 一章  函数与极限

第一节 映射与函数

一、集合

a.集合概念

概念：

• 集合（简称集）：所谓集合（简称集）是指具有某种特定性质的事物的总体，组成这个集合的事物称为该集合的元素（简称元）。

• 有限集：只有有限个元素的集合称为有限集。

• 无限集：不是有限集的集合称为无限集。

• 表示集合的方法：

• 列举法：把集合的全体元素一一列举出来表示；

• 描述法：集合M是由某种具有性质P的元素x的全体所组成的，就可表示为

• 对于数集，有时我们在表示数集的字母的右上角标上“*”来表示该数集内排出0的集，标上“+”来表示该数集内排出0与负数的集；

• 习惯上，全体非负整数即自然数的集合记作N，即

• 全体正整数的集合为

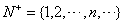
• 全体整数的集合记作Z，即

• 全体有理数的集合记作Q，即

• 全体实数的和记作R，R*为排除数0的实数集，R+为全体正实数的集。

• 子集：设A、B是两个集合，如果集合A的元素都是集合B的元素，则称A是B的子集，记作

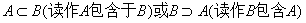
• 相等：如果集合A与集合B互为子集，即

    ——则称集合A与集合B相等，记作A=B。

• 真子集：若

    ——则称A是B的真子集，记作

• 空集：不含任何元素的集合称为空集，记作Ø，且规定空集Ø是任何集合A的子集。

b.集合的运算

概念：

• 并：设A、B是两个集合，由所有属于A或者属于B的元素组成的集合，称为A与B的并集（简称并），记作

• 交：由所有既属于A又属于B的元素组成的集合，称为A与B的交集（简称交），记作

• 差：由所有属于A而不属于B的元素组成的集合，称为A与B的差集（简称差），记作

• 全集或基本集：有时我们研究某个问题限定在一个大的集合I中进行，所研究的其他集合A都是I的子集，此时，我们称集合I为全集或基本集。

• 余集或补集：I为全集，称I\A为A的差集或补集，记作

• 直积或笛卡尔（Descartes）乘积：设A、B是任意两个集合，在集合A任意取一个元素x，在集合B中任意取一个元素y，组成一个有序对(x,y)，把这样的有序对作为新的元素，它们全体组成的集合称为集合A与集合B的直积，记为AxB，即

  
  

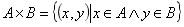
运算律：

c.区间与邻域

概念：

• 开区间：设a和b都是实数，且a<b，数集{x|a<x<b}称为开区间，记作(a,b)，即(a,b)={x|a<x<b}。a和b称为开区间(a,b)的端点，这里

• 闭区间：设a和b都是实数，且a<b，数集{x|a<=x<=b}称为闭区间，记作[a,b]，即[a,b]={x|a<=x<=b}。a和b称为闭区间[a,b]的端点，这里

• 半开区间：[a,b)={x|a<=x<b}，(a,b]={x|a<x<=b}都称为半开区间。

• 有限区间：以上区间都称为有限区间，数b-a称为这些区间的长度，从数轴上看，这些有限区间是长度为有限的线段。

• 无限区间：引进记号+∞（读作正无穷大）及-∞（读作负无穷大），则可类似地表示无限区间[a,+∞)={x|a<=x}，(-∞,b)={x|x<b}。

• 邻域：以点a为中心的任何开区间称为点a的领域，记作U(a)。

• 去心邻域：设δ是任一正数，则开区间(a-δ.a+δ)就是点a的一个邻域，这个邻域称为点a的δ邻域，记作U(a,δ)，即

    ——点a称为这邻域的中心，δ称为这邻域的半径；

    由于a-δ<x<a+δ相当于|x-a|<δ，因此

    ——因为|x-a|表示点x与点a间的距离，所以U(a,δ)表示：

    ——与点a的距离小于δ的一切点x的全体。

• 去心δ邻域：点a的δ邻域去掉中心a后，称为点a的去心δ邻域。记作

• a的左δ邻域：开区间(a-δ,a)称为a的左δ邻域。

• a的右δ邻域：开区间(a,a+δ)称为a的右δ邻域。

• 两个闭区间的直积：

    ——即为xOy平面上的一个矩形区域，

    ——这个区域在x轴与y轴上的投影分别为闭区间[a,b]和闭区间[c,d]。