波束赋形(beamforming)的数学推导（五）---- 天线间距半波长以及角域空间

这个小文章，我们仅仅从发射天线的角度来分析，通过前面四个小文章的分析，从接收天线的角度来分析，原理是一样的。

--------------------------------

录制的两个小视频：

波束赋形5_哔哩哔哩_bilibili    天线间距半波长

波束赋形6_哔哩哔哩_bilibili    角域空间

--------------------------------

如果我们指定了一个方向，则在各个方向上的接收天线，能收到的能量满足：

其中：

表示我们想指向的方向，   是一个变的量，遍历整个  到  的这样的一圈。
为了简单起见，我们不妨设 ，则：

为了只有一个指定的波束方向(这里应该理解为数学上的极大值点，应该保证只有一个波束极大值点)，则 应该介于 之间，即  在 之间，所以

我们来画图感受一下，如果

那么

则，我们对公式 1 ，按照上式来画出幅度：

在  之间只有一个最高点，在这之外，极大值点开始逐渐增大，即在另外一些方向上，也有较大的能量辐射到那个方向上。

所以，当  从 0.5 逐渐增大 1 的过程中，可以看到多出来的指向逐渐显现出来：

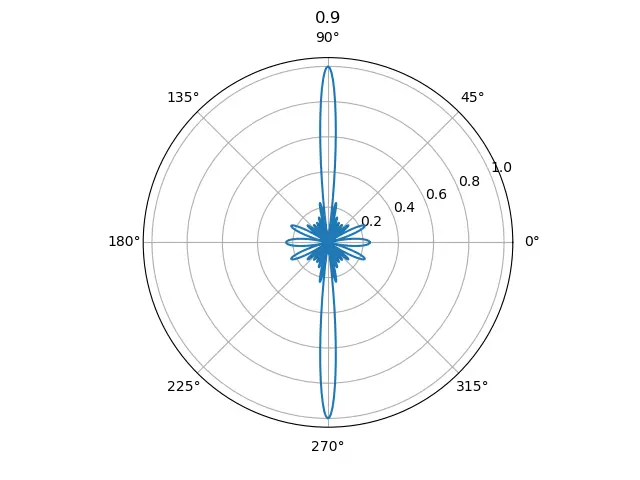
角域空间

假设有 M 根发射天线，则每个发射角，我们都可以对应一个向量：

我们知道，上面这个是一个 M 维的向量，可以认为是 M 维空间上的一个向量，由于角度的选取有无穷多个，则可以产生无穷多个 向量，既然是 M 维空间，我们应该可以找到 M 个正交向量，构成一个基，其它所有向量都可以用这个基中的 M 个向量线性组合来生成。

那，问题是，我们能保证找到 M 个正交向量吗？当然，如果没有任何限制，那 M 维空间一定有 M 个正交向量构成一个基，但是，如果我们对正交向量加了约束条件，不能任意选择，那就未必能找到。

我们加的条件是，形如公式 (3) 的向量，  取不同的值，就得到不同的向量。在这样的条件下，两个向量正交，需要两个   的取值，相差非 0 整数倍的 . 可以证明（见附录），这样的两个向量是正交的。

如果第一个向量，我们取


第二个向量取

依此类推，最后一个向量取

所以， 取值范围要大于等于 ，否则，就拿不到 M 个正交向量。

从公式 (2) 可以看到， 的范围宽度为

那么：

则：

综合以上的推导，则：

而且 M 个正交向量分别为：

这样得到了由 M 个正交向量组成的一个基。

如果

那么就不能构成 M 维空间，就会变成 M 维空间的子空间（这里有点抽象，我也不知道该怎么说得能更清楚），从“指哪打哪” 的角度来理解，就不能做到很精确的 "指哪打哪".

修改程序中变量 d_vs_lambda 的值，从 0.5 逐渐减小，看是什么效果：

在 M 维空间中，如果找不到 M 个满足上面条件的正交向量来构成一个基，那么，就是在空间“指哪打哪”的精度的损失，这一点在视频中有比较充分的说明。

附录：证明基正交

可以认为是在一个周期内求和，结果就是 0.