内模控制(Internal Model Control, IMC)的基本原理
内模控制(Internal Model Control, IMC)最早是由控制工程学者弗朗西斯(B. A. Francis)及翁汉(W. M. Wonham)所提出的,它是一种针对基于过程数学模型进行控制器设计的新型控制策略,由于它具有设计简单,控制性能好和在系统分析方面的优越性,因此它在工业过程控制中具有重要的研究意义。
目前应用最为广泛的是1982 年Garcia和Morari提出的具有模型、控制、反馈环节的内模控制结构,它的基本结构如下所示。其中虚线框里面的内容就是我们要设计的控制器,它可以通过硬件或者计算机软件实现,从下图可以发现除了控制器以外还有一个内在模型
,这也是内模控制名字大的由来。它表示的是我们对系统已知的模型,实际模型G与我们已知的模型是存在偏差的。D(s)表示的是系统的外部扰动。
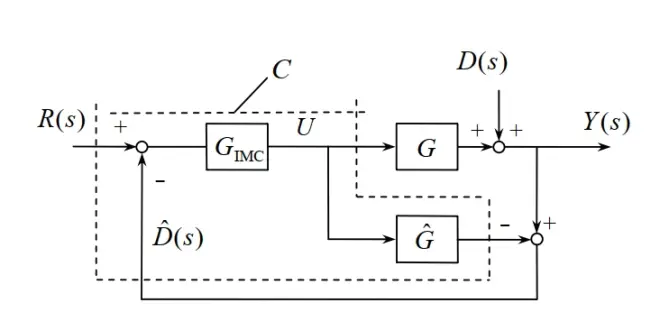
为了求得上图中的传递函数,我们将上图所示的内模控制结构等效变换为下图所示的简单反馈控制结构形式。其中的内环控制的传递函数如下图所示
相应的我们可以求得系统的闭环响应为
其中反馈信号可以表示为
当我们考虑理想系统的情况时,此时,此时系统等同于开环的状态,此时的系统的闭环响应表示为
此时的反馈信号为0,和
的稳定性决定了系统的稳定性。这时候如果我们选择
此时,系统的输出就等于系统的参考输入。这就清楚的表面了对开环稳定的过程而言,反馈的目的就是克服过程中的不确定性。事实上,在工业过程控制中,客服扰动时控制系统的主要任务,而模型不确定性也是难免的。此时,内模控制结构中的反馈信号就反映了过程模型的不确定性和扰动的影响,从而构成了闭环控制结构。 因此为了提高系统的鲁棒性,系统模型不确定性带来的影响应该最小化。由于在实际过程中这种模型的差异主要在高频处,因此,在IMC控制中加入低通滤波器则可以抑制这种不确定性。
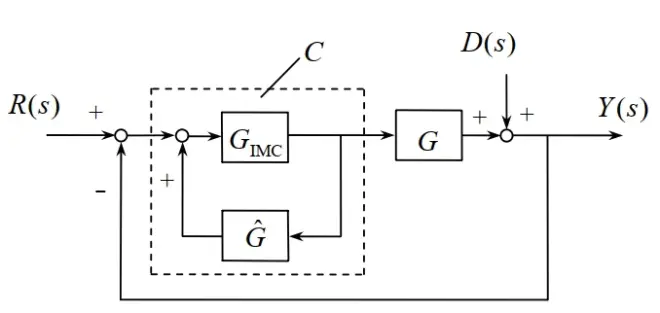
上述分析可以发现,理想控制特性是在存在且控制器
可以实现的条件下得到的。然而,实际过程中被控对象通常存在时滞和惯性环节,
中将出现纯超前和纯微分的环节,因此理想控制器很难实现。
为此,我们在设计IMC控制器时,可以分下面两步进行。
步骤一:对内在模型进行分解,分成
和
,此时
可以表示为
式中,表示不可逆的部分,它通常包含所有时滞和右半平面的零点,而
表示可逆的部分,通常具有最小相位特性。
步骤二:IMC的控制器设计
在这一步的设计,通常需要对项加上滤波器从而保证系统的稳定性和鲁棒性。定义内模控制器为
其中,表示滤波器参数,它通常影响控制系统的响应速度,
表示的是相对阶次。而
的选择要保证
在物理上可实现即可。
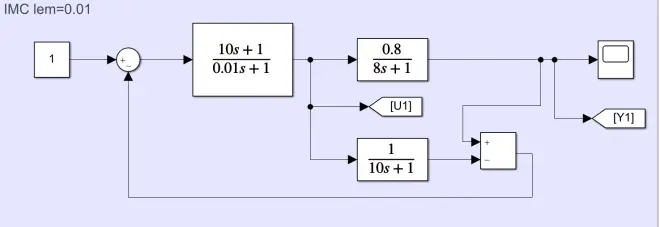
为了阐述上述方法,我们在Matlab/Simulink环境下搭建相应模型进行验证。我们首先考虑以下一阶系统
我们选择内模模型为
可以发现上述模型的逆是存在的,因此,只需要进行滤波器的设计,以保证控制器可以实现,我们选择
为一阶低通滤波的形式
则可以表示为
在Matlab/Simulink搭建的仿真程序如下
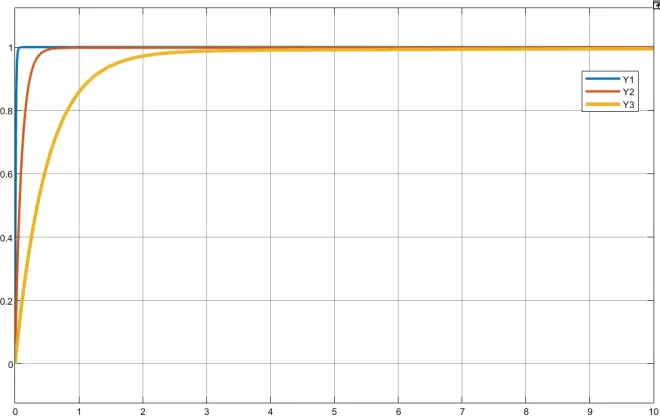
我们通过改变的值可以获得不同的响应特性,结果如下,其中Y1、Y2和Y3分别表示的是
等于0.01,0.1和0.5的情况。
此时控制器的输入U的情况如下所示
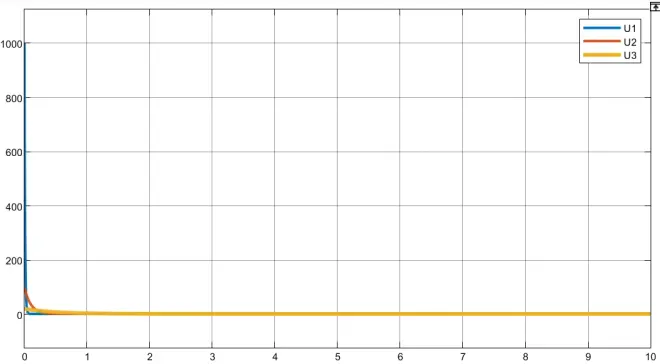
上述仿真结果表面越小,相应的速度越快。然而在实际的过程中,值过大会影响系统的鲁棒性,为了验证此理论,我们在系统的输出段加入扰动,此时的控制结构如下:
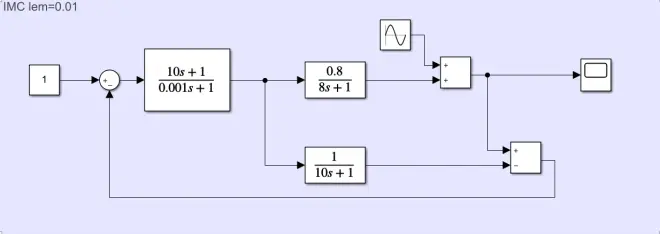
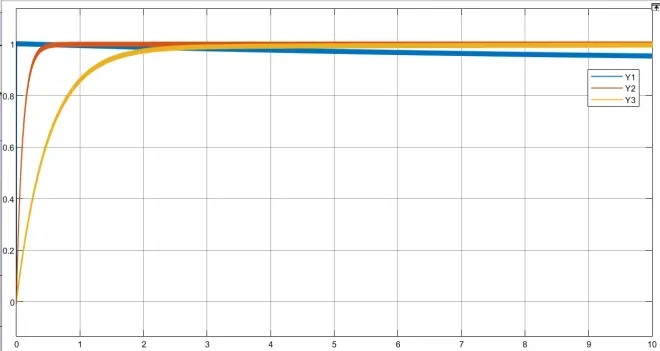
我们同样采用改变的值可以获得不同的响应特性,结果如下,其中Y1、Y2和Y3分别表示的是
等于0.001,0.1和0.5的情况。
此时控制器的输入U的情况如下所示
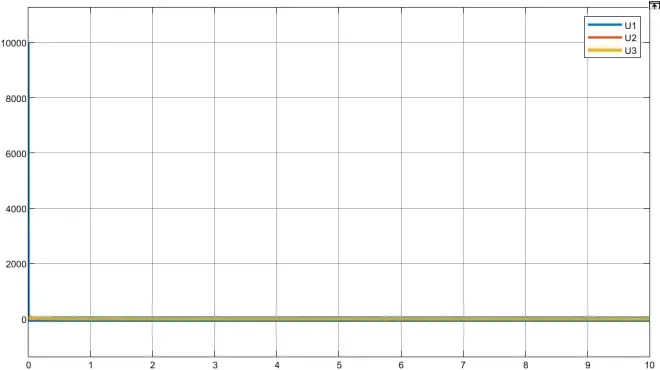
上述结果也发现此时控制输入U是波动的,因此,值的选择应该综合考虑动态响应速度和鲁棒性。

