一道集合题目的思考

最近周围同学开始学高中集合了，在做题的时候遇到了一道题，具体而言，应该是题目的答案不够详尽，题目与网上的答案如下所示。

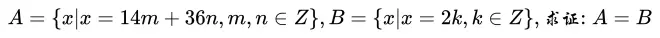
而关于这道题，在仔细思考后，发现几个比较重要的方向（最近在学高等代数）以及一个猜想。所以将这道题拿出来分享，包括自己的思路发展过程。

一、错误的开始

看到这道题的时候，我有点手足无措。因为和网上的答案类似，认为这是一个不需要证明就可以得到的结论，但是还是强行解释了一下。具体如下：

但是在我回想这道题的时候，发现了一定的错误：整数集对乘法封闭，但是取集合A={x|x=2a,a∈Z}，显然集合A包含于Z而不等于Z。对运算封闭并不能说明能取整个集合，所以这个方法证伪。

二、偶然的发现

当天下午，学习丘维声老师的高等代数，讲到第三章（和第八章合讲）的§13 集合的划分，等价关系时，丘老师用日历来举例（同时在丘老师的群表示论课程绪论中同样提到过），对整数集按照模7同余的方式构造等价关系进行划分，从而得出集合划分的抽象方法，由此我发现，这道题的证明也可以用类似的方式进行。同时，丘老师提到，在八九十年代，丘老师参与高考命题时，会选择命制证明两集合相等的题目，该类型题目的证明思路是证明两集合互相包含。由此开始本次证明。

三、正式的证明

在有了以上思路的情况下，我立刻开始书写证明过程：

四、归纳与猜测

根据上述内容的证明，我对集合划分的思想有了更进一步的认识，整数集可以通过同余的等价方式找到等价类进行划分。同时得出了一个大胆的猜想：

希望有人可以给出证明或证伪。