接续上文的内容……

Part 2 链的第二定义

现在我们来学习一种新的链的定义。

在之前的内容里，我们已经了解到了，链由两种关系构成：强关系和弱关系。它们各自的定义如下。

• 强关系：如果节点1为假时得到节点2为真，则称节点1和节点2有强关系。

• 弱关系：如果节点1为真时得到节点2为假，则称节点1和节点2有弱关系。

不过你可能会想过这样一个问题。为什么节点1到节点2的顺次逻辑，在结论里就被叙述为“节点1和节点2之间有强弱关系”了呢？难道不是“节点1到节点2有强弱关系”吗？

这个问题问得好，我们来看看如何去回答。首先，我们得了解链的新的定义方式。虽说是新的定义方式，但实际上和之前的定义是完全等价的两种不同说法而已。

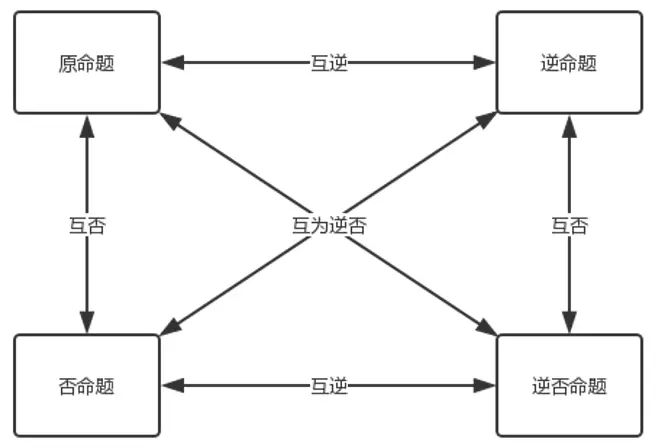
我们在高中学习过命题和逻辑一章，并了解了原命题、逆命题、否命题和逆否命题，其中逆命题和否命题真值相同（即要么都对，要么都不对）；同理，原命题和逆否命题的真值相同。如图所示。

那么，我们回顾一下强弱关系的定义，拿强关系举例，因为是证明，所以我们把命题的结论从“则称节点1和节点2有强关系”也替换为“则称为节点1到节点2有强关系”（改成有方向的）。此时我们取出其中的条件部分。

如果节点1为假，则节点2为真。

我们如果把它看作原命题，那么它的逆否命题则是把条件和结论都取反后再交换。那么命题就变为了

如果节点2为假，则节点1为真。

这两种说法明显是互为逆否命题的，所以真值相同，所以这种说法显然也可以替换到原来的强关系的定义里的，即变为

如果节点2为假得到节点1为真，则称节点1到节点2有强关系。

显然，这个说法已经把节点1和节点2互换了方向，但依然可以得到强关系。而这个逆否命题的说法显然对应的应该是

如果节点2为假得到节点1为真，则称节点2到节点1有强关系。

所以可以看到，一个条件可以得到两个方向的结论。所以强关系是不受方向的约束的，即正着推和倒着推都是可以得到结论的；同理，弱关系的证明完全是一样的。

所以，强关系和弱关系并不受到方向的约束。而链是完全依赖于强关系和弱关系的，而强关系和弱关系都可以反向推理和理解，所以链是完全可以反向理解的，故链是可以反向来推理和理解的（或者换句话说，链的两个方向推理结果都能得到一致的结论；或者干脆可以直接说链不具有方向性）。

那么，除了能够得到这一点外，我们还能得到什么东西呢？强弱关系的新的定义。

由于强弱关系都可以逆向理解，那么我们同时给出两种写法，看看有什么新的结论：

• 从节点1假到节点2真。

• 从节点2假到节点1真。

这分明说的就是两个节点不同假。因为不管两个节点哪个为假，都能推导得到另外一个节点是必须为真的，所以，强关系还可以被叙述为“两个节点不可以同为假”。

同理，我们写出弱关系的两种说法：

• 从节点1真到节点2假。

• 从节点2真到节点1假。

可以看到，不论哪个节点为真，都必须得到另外一个节点是为假的。所以，弱关系也可以被改变叙述为“两个节点不可以同为真”。所以，我们就得到了强弱关系的新定义方式：

• 强关系（新定义）：如果两个节点不同假，则称两个节点有强关系；

• 弱关系（新定义）：如果两个节点不同真，则称两个节点有弱关系。

这个说法有什么用途呢？可以看到，这种说法就可以去验证各式各样的强弱关系了，它并不受到之前共轭对等同在一个区域下的候选数的约束。我们可以利用这一点来得到一些更为奇妙的结果和结论；如果使用之前的逻辑，就不一定能得到，因为从之前的定义来看，对于ALS就显得很“无力”，因为ALS里的关系的发散的，你可以随便从之前的某个节点往下连接到ALS里的任意成立的情况，而这些情况不止一种，即并不是一种确切的情况。所以，这种新的定义模式会更加灵活、高效地把链使用起来。

不过，需要你注意的是，在新的定义里，我们完全可以察觉到一个奇妙的地方。比如强关系，我们仔细看它的定义就可以发现，“节点不同假”包含了一种情况，即“两个节点同真”，因为两个节点一共只包含四种填数可能：甲真乙真、甲真乙假、甲假乙真、甲假乙假。而不同假指的是两个节点里不能同时都是假，所以只排除了最后的一种情况，而剩下的三种情况里，是包含“同真”的结果的；同理，因为强弱关系的定义是对称的，所以弱关系还包含“同假”的结果的，所以请你务必重视，不要漏了这个特殊的情况，在某些特殊的时候，这个特殊的条件会对我们做题具有相当大的帮助，例如后面会介绍到的毛刺（Burr Rule）和毛边（Bi-burr Rule）。

Part 3 ALS的互补视角

接下来，我们来试着理解一下ALS的互补视角。

如图所示，我们先把链的文本形式写出来：

可以从例子里发现，图中存在两个ALS区域，它实际上就是一个ALS-XZ，不过从例子里看到，它并未画出之前那样合适的ALS区域；相反地，它却画出了原来ALS区域所涉及不到的单元格。这是怎么一回事？

我们这么思考这个问题。首先我们来分析c2的异数强关系r1c2(3)=r7c2(9)。我们利用新的强关系定义，如果它们同假，则c2放下3和9的位置只有r8c2一处，但r8c2显然不能同时放下3和8，所以出现矛盾，所以两个节点不同假，即形成了强关系。这一点是比较好理解的。

同理，我们再来看c9的异数强关系r7c9(9)=r2c9(3)。如果两个节点同为假，则会发现3、8、9在c9只能放在r58c9两处。显然，r58c9只有两个单元格，而3、8、9是三种数字，显然是放不到两个单元格里的，所以这样必然会产生矛盾。因此，强关系也是成立的。

这便是ALS的互补观察视角，即通过互补的角度作为占位来处理和推导矛盾：选取和原ALS涉及单元格互补的单元格，再把ALS没有涉及的数字全部圈出来，即构成互补结构。

Part 4 链式ALS结构拓展

接下来我们来看一下，套用链的ALS结构都有哪些拓展构型。

4-1 带双RCC的ALS-双强链法则

如果我们之前学到的ALS-XZ并不够新奇的话，我们现在就来接触一种新的ALS-XZ，而这种结构更为特殊。

在此之前，我们先来介绍一个术语：严格共享候选数（Restricted Common Candidate，简称RCC），这个词在一些软件和分析ALS技巧里经常使用。

我们先来说说RCC是什么。RCC实际上指的是之前ALS-XZ里的那个X，即弱关系连接的候选数。也就是说，一般来说ALS-XZ只有一个RCC（因为ALS-双强链法则规定了链只有一个弱关系，故只可能有一个RCC），例如第一个示例里的1和第二个示例里的8，就是RCC。

那么，ALS-双强链法则是否可能产生两个RCC呢？答案是可以，不过因为从结构上根本不可能实现两个弱关系，那么怎么形成呢？我们来看下面这则示例。

如图所示，我们把r2c239看作一组ALS（三个单元格，有2、4、7、9四种候选数），r4c23看作一组ALS（两个单元格，有1、2、4三种候选数）。这个链的写法如下：

或

这个结构可以写成两个不同的链结构。也就是说，这个结构自带了2和4两个RCC。根据原定的ALS-XZ逻辑，那么可以删除掉的是c2内其余单元格的候选数2，以及c3内其余单元格的候选数4。那这题为啥标注了那么多红色的删数？

回想一下RCC的特征：RCC呈弱关系，意味着两数不可同真。不可同真本应该指的是“同假”或“有且仅有一个为真”，但是当我们删除掉c2内其余单元格的候选数2和c3的其余单元格的候选数4之后，RCC就不可能再同假了。因为删掉这些数之后，c2其余位置就不再存在填入2的地方，c3的其余位置也就不存在填入4的地方，此时RCC变为共轭对。共轭对即一真一假，比如图中r24c2(2)这个共轭对，只能是一真一假，r24c3(4)也是一样的情况。首先，我们根据上面描述出来的两条链，可以看到两个强关系：

• r2c2(2)=r2c3(4)

• r4c2(2)=r4c3(4)

这意味着r2c2(2)和r2c3(4)不可同假，同时r4c2(2)和r4c3(4)也不可同假，而且r24c2(2)和r24c3(4)又都只能是一真一假。这样的话，r24c2(2)和r24c3(4)这四个候选数的填数情况只可能是以下两种可能了：

• r2c2(2)和r4c3(4)同时为真；

• r2c3(4)和r4c2(2)同时为真。

别无其它可能。这样一来，观察r2c239这组ALS，里面的r2c2和r2c3其中有且仅有一格被RCC数字占据。那么，ALS内其余两格，则会构成79数对。同理，r4c23这组ALS，里面的r4c2和r4c3其中有且仅有一格被RCC数字占据，剩下一格就一定是数字1。也就是说，结构r2c239（靠上方）这组ALS一定会产生79数对，r4c23（靠下方）这组ALS一定会产生数字1，所以r2的其余位置都不应该填入数字7和9，r4和b4内的其余位置也都不应该填入数字1，因此删掉它们。

这个结构分析起来非常复杂，因为带有了两个RCC，并且组成了特别的结构。

它的名字是什么呢？带有双RCC的ALS-XZ（Doubly Linked ALS-XZ）；而对比这种说法，最开始的结构因为只有一个RCC，所以可以被称为带有单RCC的ALS-XZ（Singly Linked ALS-XZ）。

4-2 ALS-XY-Wing

4-2-1 普通的ALS-XY-Wing示例

在之前的Wing结构一节里，我们介绍了一些Wing的链式写法，其中提到了XY-Wing，那么我们来看看ALS可否和XY-Wing交织形成新的东西。

如图所示，链的写法如下：

在例子里，为了简化涂色逻辑和思维，而且我们也讲到了互补的视角，所以图上全部都是ALS的互补视角的绘制逻辑。

如果{r1c789, r3c9}(2)和r1c78(9)同假的话，则可以发现b3里能放下2、4、9的位置只有两个单元格，出现矛盾；同理，如果r1c12(9)和r3c3(7)同假的话，则b1里放7和9的位置只有一个单元格可填，出现矛盾；如果r6c3(7)和r6c7(2)同假，则r6里只有一个单元格能放2和7，也是放不下的，出现矛盾。

所以，所有强关系都成立。不过，为什么它跟XY-Wing沾边呢？从这个链涉及的候选数的顺序来看，是2=9-9=7-7=2，和XY-Wing的链的写法完全是一样的，所以这个结构就叫做ALS-XY-Wing。

4-2-2 ALS区域有重叠的ALS-XY-Wing

我们再来看一则示例。

如图所示，这个链看起来比较混乱，因为有一部分ALS和ALS是重叠的。我们先写出文本表达：

这个示例一共是涉及了三个ALS区域，而其中最容易理解和明白的ALS区域是{r5c6, r6c56}(1245)和r2c356(1568)。实际上，b2里有一个ALS区域是{r1c45, r2c56, r3c456}(12345689)。这个区域稍微大了点，涉及了七个单元格，并包含了8种数字，但也确实满足ALS的要求，所以也是合格的ALS。

别看数很多，逻辑还是很清晰的。如果r2c36(8)为假，则r3c6(1)必须为真，否则紫色的ALS区域里将少掉两种数字1和8，使得四个单元格仅填两种数字，显然是不够填的，所以产生矛盾；而第二个ALS区域就不用过多分析了；第三个ALS因为涉及了7个单元格，所以显得很复杂。从之前的逻辑，我们推理到了r2c5(5)为假，则r3c46(8)此时必须为真，否则的话，在这个区域里其余位置也没有其它的5和8，所以会少两种数字，7个单元格就只能填入6种数字，导致填数不够的矛盾。所以强关系是成立的。

此时，这个例子特殊的地方仅仅是，ALS区域有重叠，导致了理解起来的不便；不过针对于这种例子，我们可以尝试使用互补视角来观察：如果5和8都去掉后，b2里只有r2c4能放下5和8，而显然是不能同时放下两个数的，所以矛盾。

4-3 ALS-双值格链

接下来我们再看一则更长的ALS链式结构。

如图所示。

这个链内一共有四个ALS区域，它们分别是r1347c8、r9c34568、{r7c1, r9c2}和r2c126。分析方式和之前的ALS-XY-Wing等结构相同，这里就不再重复。强关系依然采用“不可同时为假”进行分析。不过，如果你觉得这种结构过大的话，可以试试互补视角，不过互补视角后，部分位置就会产生重叠。如图所示。

5-4 ALS-W-Wing

接下来再来看一则示例。

如图所示，链如下所示：

这个链内一共有两个ALS，并且位于首尾。所以利用刚才的结论，我们可以知道，r7c23(8)和r7c23(1)是强关系。同时为假的时候，r7c23内只有3这一种候选数可填，这显然不成立。结尾的强关系也是一样。

这个结构的写法非常类似于W-Wing的结构：(w=x)-x=x-(x=w)，所以被称为ALS版本的W-Wing，即ALS-W-Wing。

4-5 死亡绽放

接下来我们来说一个和Wing里分类讨论模式非常相似的ALS技巧：死亡绽放（Death Blossom）。

4-5-1 三个花瓣

如图所示，图中一共使用了两个ALS区域：r23c45(23567)和r239c5(2467)。

我们按r7c4作为拐点进行分情况讨论。

• 假设r7c4 = 3，则由于r3c4 <> 3的关系，如果此时橙色ALS里如果没有2，则会少两种数字，便出现错误，所以{r2c45, r3c5}(2)为真；

• 假设r7c4 = 4，则r9c5 <> 4，如果此时r239c5(2)全部消失，则红色ALS里同时少了两种数字，导致不够填的矛盾；

• 如果r7c4 = 5，和第一个情况类似，得到橙色ALS里无法填数。

所以，由于三种情况都可以得到2为真的结果，而r7c4只有三种情况，所以{r2c4, r239c5}(2)里必须至少有一个数字2为真，所以删除掉这4个2的交集。

在死亡绽放里，我们把类似于Wing类分支情况的技巧里的拐点或折点称为花瓣单元格（Petal Cell），这个单元格有几个候选数就称有几个花瓣。比如该示例里有三个候选数，即三个花瓣。

4-5-2 四花瓣

如图所示，我们按r9c1进行分情况讨论。

• 假设r9c1 = 2时，r8c23 <> 2，如果r8c6 <> 5则在橙色ALS里少了两种候选数，导致填数不够，所以r8c6 = 5；

• 假设r9c1 = 4，则红色ALS，可以得到r8c6 = 5；

• 假设r9c1 = 6，则绿色ALS里必须让r6c7 = 5，否则绿色ALS里少两种数字，不够填数，出现矛盾；

• 假设r9c1 = 7，则橙色区域和情况1一样，r8c6 = 5。

所以，不管是什么情况，最终必须r6c7或r8c6里至少有一个单元格是5，所以删除其交集，即r8c7(5)。

这个示例带有四个花瓣。一般来说，三个花瓣的示例找起来就比较困难了，所以一般四个花瓣的很少发现，甚至发现不了，所以仅供参考和学习。

4-5-3 五花瓣

如图所示，这个示例带有5个ALS区域（分别用红色、橙色、绿色、蓝色和紫色五种颜色来表示，注意r3c6被三个ALS区域共用），也恰好有5个花瓣。不过这个例子依然和之前的推理方式一致，所以我们此处不再重新推理，不过题目很漂亮，可以拿来学习和参考。

4-5-4 六花瓣

请自行推理。

4-6 带ALS的链

4-6-1 普通的例子

如图所示，这个链的写法如下：

如图所示，这个例子就不用过多解释了，它的原理和之前的ALS完全一样，只是注意一下c9的ALS，此处画出的是它的互补视角：如果同假后，2、6、7将只能放在两个单元格里，显然不够填，导致矛盾。

4-6-2 假SDC的强关系

之前我们说过SDC技巧，但是我们从来没有想过，把SDC插入到链里使用。我们来看看SDC如何放到链里去灵活使用。

先来看第一个示例。

这是一条长为1的链，没错，它只有一个强关系构成，虽然这一点有点别扭，但实际上在链的定义和叙述里，我们明确说到“以强关系开头结尾，并且奇数长度”。这个例子确实强关系开头也是强关系结尾（只是它们都是同一个强关系），而1确实也是一个奇数。

这条链的逻辑很简单，r1c7(1)和r8c8(1)不同假。那为什么不同假？如果把它俩去掉，则一个看起来像SDC的结构{r13c7, r238c8}五个单元格仅包含2、3、6、7，而且全部的数字都不跨区出现（2、3只出现在b3里，6、7只出现在c8上）。这显然是一个SDC结构了。不过试想一下，如果所有数字都不跨区，而且还没有一样的数字，就意味着这些数必须有且仅有一个，不多也不少。可是，这一共是五个单元格，却只有2、3、6、7四种数，使用SDC的跨区数组的逻辑是完全填不满的。是的，这就意味着SDC就直接自动出错了。故假设错误，即r1c7(1)和r8c8(1)必须至少有一个为真。

可以看到，这里的SDC实际上是一个假的SDC，根本就经不起推敲。五个单元格只有四种填数是显然直接出错的，而这种结构只是长相很类似SDC，所以这里把这个结构称为假SDC（Fake SDC）。

这种假SDC在链里很喜欢出现，而且这种结构在使用的时候会非常灵活。而且，这种结构跨区域产生了强关系，非常厉害。

接下来我们再来看一则示例。

如图所示，表示如下。

最难理解的地方就是这里的SDC两端的5的节点。我们假设r1c6(5)和r1c2379(5)同假，则在{r1c2379, r3c3}里只剩下2、3、4、8，而且2、3只出现在r1上，4、8只能出现在b1里。并且涉及五个单元格，但五个单元格无法填入2、3、4、8四种数字，所以出现矛盾。故这两个关于5的节点不同假。

4-6-3 节点重叠

这个示例有些奇葩，链如下所示：

这个链头r3c13(7)和链尾r23c1(7)都是7的区块。不过有些特殊的是，r3c1(7)被两个区块组共用。不过，删数也是存在的。因为r3c13(7)和r23c1(7)至少一个为真，意味着这三个单元格的候选数7，至少都有一个位置是为真的（r3c1(7)为真，就是这个特殊情况）。删掉交集，也就是b1的其余位置的7啦。

之前说到过，节点不一定只是候选数，也可以是区块，所以这里的链头和链尾就是两个区块了，它们有部分重叠，所以称为节点重叠。

当然了，节点重叠并不一定是区块和区块之间，也可能是ALS内部产生的部分之间的重叠。比如这个例子：

其中，r48c8(7)=r8c8(8)是产生于r48c8内的ALS，而r6c9(8)=r4c8(7)则是产生于{r4c8, r6c9}的ALS。

这个结构就比起刚才的难观察一些了。