郑涛（Tao Steven Zheng）著

【问题】

调和级数（harmonic series）是由倒数和（sum of reciprocals）给出的无穷级数（infinite series）。

题一：使用比较判别法（comparison test）来证明调和级数发散。

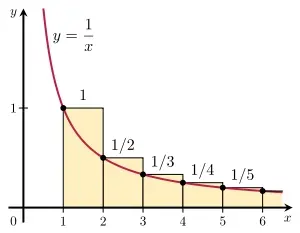
题二：使用积分判别法（integral test）来证明调和级数发散。

【题解】

题一: 比较判别法

把调和级数中的项分组成：

上面分组的每个括号总是大于 ：

因此，

由此可见

所以

题二: 积分判别法

因此

【历史纵横】

题一的方法（比较判别法）是中世纪法国神学家、哲学家和数学家尼克尔·奥雷斯姆（Nicole Oresme，约公元 1325年 - 1382年）的证明。