数学实现信号分析[ω]: 关于傅里叶的一些奇奇怪怪的捷径

这篇就是傅里叶相关的最后一篇专栏了, 当然傅里叶远不止这么点东西, 还有更多更多的知识等待被大家学习哦

FF.....FFFFFF

在高维傅里叶变换中, 其实有一个懒人计算方法

假设有一个n维函数(或序列), f(x1, x2, ..., xn), 那么整个傅里叶变换可以这样算:

首先在x1方向对每一行进行一维傅里叶变换, 然后在x2方向再进行一次一维傅里叶变换, 以此类推, 最后在xn方向进行一次傅里叶变换

最后的结果与直接计算高维傅里叶变换的结果是一致的

证明:

F [f(r+r0)] (ω)

现实中总会遇到以下的情况: "已知有一个n维的函数f(或序列), 但是我们已知的起点是不在中心的(0, 0), 我们需要求出f经过一段位移r0的傅里叶变换", 其中最常见的就是图像变换, 我们理解的坐标原点是在图像中心, 但是计算机理解的坐标原点是在图像的左上角, 这时候就要进行相应的变换

同理, 逆变换也有相应的操作:

特别地, 需要注意一下, 在离散傅里叶变换中, 整个原序列 x 都是在n维的空间 [0, 1)^n 中, 但是经过傅里叶变换后的频率序列是在 [0, w)^n 中的

例子: 假如现在有一副100*200的图片, 那么这副图片所占用的空间为 [0, 1) * [0, 1), x方向两点间隔为1/100, y方向两点间隔为1/200; 而经过傅里叶变换后的频率序列占用的空间为 [0, 100) * [0, 200), x和y方向两点的间隔都为1

 注意: 在离散傅里叶变换中, 使用这种方法进行位移的话会出现 "循环位移" 的现象, 也就是说原版应该被移动到序列范围外的数据点, 会再次出现在移动方向相反的地方, 例子:下面是一副744x906x3的图片, 现在对这个图片进行(400, 400)方向的位移, 得到结果:

卷积 Convolution

学神经网络的别兴奋, 此卷积非彼卷积, 这个是数学上严格定义的卷积运算, 神经网络的卷积是因为和数学卷积类似才有了卷积这个名字而已

以下定义卷积运算:

卷积运算在工程上用处非常非常大, 只要选择合适的核函数g, 在图像方面可以用作模糊化, 在音频方面可以用作降噪

但是在计算机中计算积分可不是一件容易的事情, 通常要等上几十秒或者几分钟才可以出结果(这里用蛇py做例子), 于是就有了下面的快速计算方法:

证明: (这里使用一维, 因为实在不想打字了, 写公式好麻烦= =)

导数的傅里叶变换

f(t)的n阶导数的傅里叶变换可以由以下方法求出:

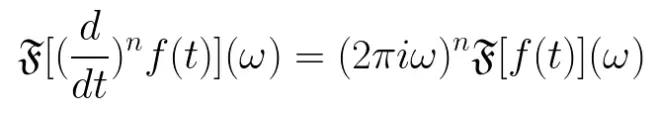
这里我只证明第一阶求导, n阶其实就是重复求导而已

Plancherel定理

在物理中经常会提到系统的能量, 并且单一频率的能量正比与这个频率的平方

在傅里叶变换中存在保范性(因为还没说过函数空间, 所以这里可以理解为能量守恒):

这也就是说变换前后的能量不会发生变化

证明:

关于分部积分: