【银蛇出品】数学漫谈6——日经题之有理函数不定积分的通解

前置知识：不定积分、多项式、复数的基本运算

        最近经常能看到这样一类问题：

我们称之为日经题。下面分享一种这类有理函数不定积分问题可套路化的通解的思路。

        首先说明什么是有理函数。有理函数是指形如p(x)/q(x)的函数，其中p(x), q(x)为关于x的多项式，并且q(x)的次数高于p(x)。前述三道例题中的被积函数就是有理函数，再如，x/(1+x²)也是一个有理函数。也就是说，有理函数的通式为

其中am, bn≠0且n>m。

        不过，问题并没有得到简化，我们需要引入一些定理来帮助我们解决问题。

        代数基本定理十分著名，它的内容如下：在复数域C内，n次复系数多项式必有n个根。代数基本定理最早较为严格的证明由Gauss给出，迄今为止已有200余种证法。不过这里我们不证明它，但它对于我们接下来的推导十分有用。代数基本定理说明，一个n次多项式在复数域内必然可以写成

其中zk(k=1,2,…,m)为该多项式的m个复根。当然，这里面zj=zk(j≠k)是被允许的，这时zj或zk就是重根。

        接下来在实数域R内考虑，即令ak(k=1,2,…,m)全为实数。任取其中一个复根zk，设zk=xk+iyk，回代公式(2)中应有

而若将zk的共轭zk*，也就是xk-iyk回代公式(2)中则有

对比公式(3)(4)中的两项系数，可以发现公式(4)的结果也是0。这就是说，对实系数n次多项式，若zk为其复根，则其共轭zk*也为其复根。这样，若公式(2)等号右端乘积项出现了(z-zk)，那么同时(z-zk*)也必然出现。又因为

即在公式(2)等号右端，可能存在一对一次多项式，它们的积能够写成一个实系数二次(不可约)多项式。也即实系数n次多项式一定能写成若干实系数一次多项式和二次(不可约)多项式的乘积

其中i+2j=m。

        利用这个性质，我们可以将公式(1)的有理函数进行分解

其中i+2j=n。公式(7)中各项分子系数可由待定系数法确定，即对分解结果进行通分，然后分子加和与原式逐项对应。

        至此，我们已经把有理函数不定积分的问题归结为：如何求如下形式的6种不定积分

其中n=2,3,…，a, p, q为实数。

        第1、2、3种不定积分求起来比较容易，直接给出结果

        第5种不定积分经简单转化可化为第3种不定积分

        第6种不定积分经简单转化可化为第4种不定积分

         第4种不定积分可以利用分部积分法降次，最终转化为第3种不定积分

证明 利用分部积分法

        移项，整理得

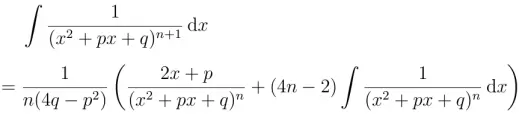
        用n-1代替n即得公式(13)。

        这样，有理函数不定积分的问题就都能被解决了。下面我们解决两个例题。

例1 求不定积分

解    方程z⁵+1=0的五个根依次为

        于是

        于是设

        解出(其实很不好解)

        于是

例2 求不定积分

解    由公式(12)