背景

考虑以下实际问题：为验证一种药物的作用，实验组使用该药物（结果遵从分布F），对照组使用安慰剂（结果遵从分布G）。结果的两组数据的对比，希望知道F和G之间有多少差异，即：这种药物有无效果（假设检验角度）/作用大小的估计（区间估计角度）[假设检验和区间估计是对偶的]。

这两个组之间可以是independent的，也可以有pairing。

用上一篇文章的asymptotical test方法构建asymptotical test以及asymptotical interval estimation都是可行的。不过我们现在需要针对这种实验组-对照组问题develop一些特定的test statistic来统一地做假设检验和区间估计。

相同已知方差的正态族

本节考虑以下模型： 

我们打算考察的量是$\mu_X-\mu_Y$（假设检验/区间估计）。

如果方差是一个给定值，则很自然地可以设计一个用于假设检验/区间估计的（标准化）统计量（这就是Wald test的思想）： 

Z服从标准正态分布$N(0,1)$，所以可以算level。接下来如果要假设检验$H_0:\mu_X-\mu_Y=\theta,H_1:\mu_X-\mu_Y\neq\theta$，则拒绝域可以取为

把这个拒绝域对应的接受域invert一下就变成估计区间了。事情就办完了。

相同未知方差的正态族

如果方差不是给定值，我们得把上面统计量的$\sigma$换成一个estimator。为了用上X和Y的所有信息，我们需有用pooled sample variance：

也就是两个sample variance的加权平均。也可以这样理解：分子就是全部(X_k-\bar{X})^2求和，而分母本来应该是m+n，但是去掉了两个自由度（分别来自\bar{X}与\bar{Y}），所以是m+n-2。

于是我们需要的统计量为

这个（准确的）分布很容易通过t分布的定义得来。这样一来，假设检验和区间估计就都好办了；而且它们都是exact的test，不是asymptotic的。

我们可以再具体地看one-sided和two-sided的假设检验。$H_0:\mu_X=\mu_Y$表示药物不起作用，而备则假设可以为：$H_1:\mu_X\neq\mu_Y, H_2:\mu_X>\mu_Y, H_3:\mu_X<\mu_Y$。我们使用的检验统计量为

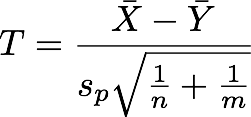
三种备则假设的拒绝域分别为

补充一句，前面的H_0 versus H_1的拒绝域和LRT构建出来的是一样的。验算一下即可。

不同未知方差的正态族

这个问题是著名的Behrens-Fisher问题。前面的T统计量中的\sigma不能再用了。所以Fisher转而采取这样一个最简单的归一化形式的统计量：

这个统计量的精确分布是很复杂的（上下同时标准化之后，上面是正态，下面看起来像个卡方，但是实际并不是；不过我们可以近似看成卡方，其自由度由Welch–Satterthwaite equation给出，这样T的分布就是近似t分布了）。不过它可以近似为以下自由度的t分布（一般不是个整数，当然t分布的自由度也未必非得是个整数；不过一般大家把它round到最近的整数上去） 

这个式子怎么记呢？它形式上就是从T的分母来的，并且大致是n-1或者m-1的大小）注意：这个时候事情变得有些微妙…以前T统计量的分布是只取决于n和m的，但是现在还包含进了方差，但是方差我们是不知道的。所以在做假设检验/区间估计的时候，我们还得用样本方差去估计这个自由度。但是这不过是一个近似方法，所以问题也不是很严重。只是在数学上，这样一个解并不是很完全。上面这种解法称为Welch–Satterthwaite solution，也叫做Welch's t-test；还有其他人给出了不同的solution，比如Fisher用他的fiducial inference给了一个基于Behrens–Fisher distribution的解；还有Bayes方法的解等等。但是这个问题迄今还没有令人完全满意的解答。wikipedia里面把这个问题列为经典统计学里面的一个尚未解决的问题：Is an approximation analogous to Fisher's argument necessary to solve the Behrens–Fisher problem?Yuri Linnik showed in 1966 that there is no uniformly most powerful test for the difference of two means when the variances are unknown and possibly unequal. That is, there is no exact test (meaning that, if the means are in fact equal, one that rejects the null hypothesis with probability exactly α) that is also the most powerful for all values of the variances (which are thus nuisance parameters). Though there are many approximate solutions (such as Welch's t-test), the problem continues to attract attention as one of the classic problems in statistics.

最后，如果underlying distribution不是正态，那么如果样本数足够多，上面的Welch's t-test还是能用的（CLT保证了）。

Mann-Whitney Test (Wilcoxon rank sum test)

这是一个非参数统计方法。秩和检验是建立在排序（rank）上的，所以所有保序变换都不影响检验的结果（比如比较两组人的分数是否有显著差别，调分前和调分后检验结果一样；除非像某课一样出现非保序调分）。

秩和检验的setting是这样的：我们有n个对照组数据X_1,…,X_n，m个实验组数据Y_1,…,Y_m。零假设是：实验组与对照组分布相等。

思想很简单：我们把m+n个样本排序，把某一组（比如实验组Y）里面的排序加起来，得到统计量T_Y。如果零假设成立（不管是什么分布，只要两个分布相等），那么这个T_Y应该大概率在“中间”，不会很大或者很小（跟p值的想法一样）：如果很大，就说明Y大量排在X后面，即Y显著大于X；反之亦然。这个“中间”具体这样算：T_X+T_Y=(m+n)(m+n+1)/2，其中T_Y是m个和，如果均匀分配的话应该分配到m(m+n)，于是ET_Y=m(m+n+1)/2。当然T_Y的具体分布是能算出来的（而且跟F与G完全无关），于是接下来做假设检验和算p值都是轻松的。

因为秩和检验只算秩，所以它对outlier（在基因测序中很常见）是不敏感的。比如一个最大值100被测成了10000，秩和检验不会受到影响（但是Welch’s t-test会有比较大的影响）

我们还希望对大样本有渐进分布。这个渐进定理类似于普通的CLT（不过并不是CLT，因为不是i.i.d）：

这个渐进在m和n都大于10时就已经非常精确。关于均值和方差的计算，自己算就行了（不放回摸球模型）。均值可以直观地看出来，方差必须得算。

秩和还有另一个等价的刻画。我们考虑用概率P(X<Y)来考察药物的作用效果。如果没有效果，它应该是1/2。概率越大，表示作用效果越强。一个自然的estiamtor为

经过简单的计算，可以发现这个estimator可以用秩和检验统计量来表达：

这个计算说明“秩和统计量”和“X_i<Y_j的个数”这两个统计量是等价，或者说可以相互转换的，我们可以按照具体情况选取合适的一个。

虽然看起来不太像（似乎只能检验两个分布一样？），但Mann-Whitney test还可以用于区间估计。技巧是平移。假设使用药物之后，概率分布做了一个平移（这是最简单的情况）\Delta。我们希望得到\Delta的置信区间估计。前面的计算说明：rank之和T_Y(T_X)与X_i<Y_j的个数U，这两个统计量之间是可以互相转换的。现在我们用后者更加方便。在渐进情况下，U自然也是一个高斯分布，所以通过inverting a test可以得到\Delta的区间估计为

最后有一些技术层面的说明：

• 如果排序中出现了tie，怎么办？（tie在比赛里的意思是：If two people tie in a competition or game or if they tie with each other, they have the same number of points or the same degree of success.）如果tie的数量比较少，就assgin average rank，不会有显著的影响。如果tie的数量比较多，就需要modify了，查文献去。在signed rank test中也是一样，|D_i|排序时若出现tie，则需要对rank平均，

• 虽然Mann-Whitney test中不会出现，但这里还是提前说：在signed rank test中，如果difference出现0，没法排序，就把这些pair直接扔掉。

还有一个说明：秩和统计量有两种形式，一种是rank sum，一种是X_i<Y_j的个数之和。这二者之间的灵活转换是很有用的。比如说，rank sum的分布是很难求的，但是X_i<Y_j的个数之和这个表达就变成了若干简单的随机变量之和，算期望、方差之类的就非常简单。我们甚至可以玩一些更夸张的花样。比如说，如果零假设不成立，F和G是两个不同的分布，rank sum的期望和方差是什么呢？乍一想，这个问题非常困难，要把每种排序遍历过去，再把这些概率加起来。但是如果我们吧rank sum写成X_i<Y_j的个数之和这种等价形式的话，这个问题就简化了很多。举个例子，X_1,...,X_n服从N(0,1)，Y_1,...,Y_n服从N(1,1)，则X和Y混合的rank sum服从什么分布呢？利用上面的技巧，我们可以算出

这个结果不仔细思考过的话肯定会觉得不可思议。感兴趣的读者不妨用数值计算来验证这个结果。

Comparing Paired Samples 

paired sample的情况可能出现在：同一个样本前后两次测量；同窝出生仔畜采取不同的处理，等等。此时X_i与Y_i是成对dependent的。下面看到，因为pair的存在，这种情况其实更简单。

首先，模型的设定是这样的。样本对是(X_i,Y_i),i=1,…,n。不同对之间是i.i.d.的，每个对里面的分布刻画为\mu_X,\mu_Y,\sigma_X^2,\sigma_Y^2,\sigma_{XY}=\rho\sigma_X\sigma_Y。我们要考察的仍然是药物作用\mu_X-\mu_Y。

和前面一样，我们有基于正态假设的t检验与非参数的rank test。

首先是基于正态假设的检验。很简单，处理i.i.d.的D_i=X_i-Y_i，由此构建t统计量即可。（为什么这时候这么简单呢？因为可以成对地处理啊。我们要考虑作用前后的差，那么每一对前后作差是很自然的。前面m和n一般是不相等的，所以没法这么玩）

然后是非参数检验。一样的思想，我们还是考虑成对的差。这样构建统计量W_+：先把差D_i取绝对值|D_i|排序，然后把排好的序加上差的符号（如果有0，就丢掉）。其中正的秩和记为W_+。如果零假设成立，W_+与W_-大致是绝对值相等的，它们都不会太大或者太小。

一样的，我们有渐进行为：（均值很直观，方差得仔细求）

实验设计方法

关键词：对照组，双盲实验，安慰剂效应，随机化分配。具体的例子可以看Rice的书。

Concluding Remarks

本文研究的问题在科研中是非常普适的。当我们设置实验组和对照组后，我们需要比较结果。对于物理或者化学，结果的比较通常还是比较清楚的；但对于生物或者医学，结果的随机性可能很大，此时就必须要引入统计方法来研究实验组和对照组到底在多大的可信程度上有多大的差距。

关于Bayes角度的样本比较，就不写了。

前面讨论的方法可以分为两种：基于正态假设的参数检验（利用t统计量）与非参数检验（利用秩和统计量）。神奇的是，即使正态假设成立，秩和检验仍然更加powerful。Lehmann (1975) shows that the efficiency of the rank tests relative to that of the t test—that is, the ratio of sample sizes required to attain the same power—is typically around .95 if the distributions are normal. 也就是说，100个样本的t test与95个样本的秩和检验能够达到同样好的效果。这件事情非常反直观，而且也说明秩和检验是个好东西，是preferable的。

总结一下两种方法总的思想：

比较两个样本之间的差距，总的做法有两种：参数的t-test与非参数的秩方法。参数方法建立在正态假设下（不过大样本时非正态亦可），其思路是（和Wald test一样）构建一个零假设下标准化的“N(0,1)”来做检验和区间估计。具体实行起来，因为方差不知道，所以技术上需要一些新的东西，比如Welch–Satterthwaite的solution。秩方法则非常直观，利用排序（或者等价的，多少个X_i<Y_j）来做检验。再加上平移技巧，它还可以用来做区间估计。如果是paired-sample，事情更加简单，因为我们可以直接成对作差做t-test和rank test。于是我们实现了最终目标：给定实验组和对照组的数据，推断“药物作用”的区间估计。