AB=3，DE=4，直角三角形ABD和CED，求绿色阴影部分面积？

题目：
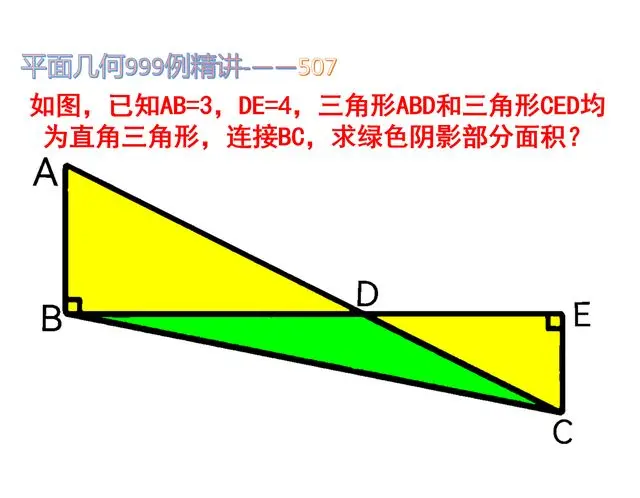
如图，已知AB=3，DE=4，三角形ABD和三角形CED均为直角三角形，连接BC，求绿色阴影部分面积？

粉丝解法1：
连AE，AB∥CE，s绿＝s△BCD＝s△ADE＝1/2xDEⅩAB＝1/2x4x3＝6。

粉丝解法2：

粉丝解法3：
连接AE，阴影面积=三角形AED面积=3*4/2=6。

粉丝解法4：
由已知条件可得，Rt▲ABD~Rt▲CED,
AB:CE＝BD:DE,
BD×CE=AB×DE=3×4＝12,
所以,
绿色阴影部分面积=BD×CE÷2＝12÷2=6.

粉丝解法5：
△ABD与△CDE相似,
AB/EC=BD/DE,
BDXEC=ABXDE=2S△BCD=3x4=12,
S△BCD=12/2=6。

粉丝解法6：
3/BD＝CE/4，→
S＝BD·CE/2＝6

粉丝解法7：
连接ae，根据蝴蝶定理阴影面积等于三角形ade的面积，3✘4✘1/2=6

粉丝解法8：
令AD为m，Ec为n，s阴为a，连AE，则有s△ADE＝s阴a， 3：m＝n：4→mn＝12 a^=3m÷2x4n÷2 ＝12mn÷2＝3mn ＝36 a＝s阴＝6。

粉丝解法9：
解:连结AE得，S阴=S△ADE（蝴蝶）=4X3/2 =6（cm^2）。

粉丝解法10：
三角形ABD相似于三角形CED，所以AB/CE=BD/DE，即3/CE=BD/4，所以BD•CE=3X4=12，阴影部分面积=BD•CE÷2=12÷2=6cm^2