40分钟构建 椭圆题型、方法体系！

椭圆

知识体系图👇

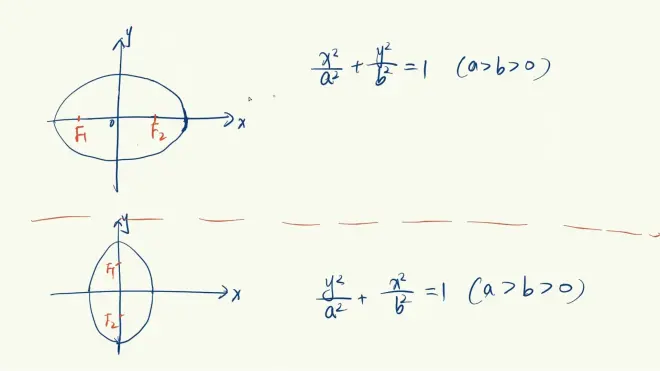
重点知识回顾：较大的那个数上是谁（x或y）焦点（F）就在哪个轴上👇

对于公式需要知道

1.椭圆的定义: m+n=2a(考的较多)

2.半焦距c和a,b之间的关系：—————（经常当作隐藏条件，缺少方程式，可以考虑）

3.离心率公式：————👇

焦点在y轴和在x轴上一样

几何性质

题型Ⅰ.几何类

1.定义（较为简单）

2.定义+几何

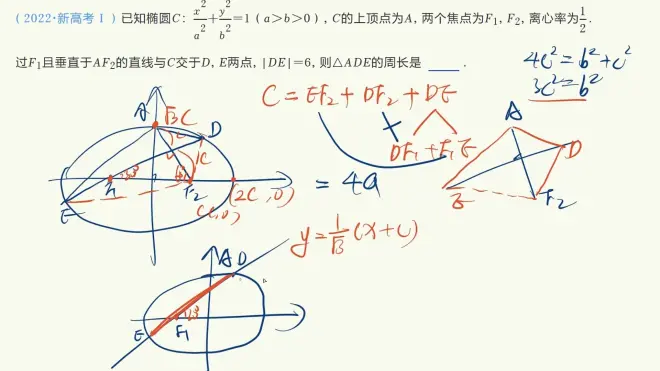
由椭圆上一点和两个焦点组成的问题：焦点三角形问题（考察的较多）

此题也可用圆与椭圆相交联立解方程（计算量不算大）

3.定义+几何+辅助线（很多椭圆的辅助线都是将椭圆上的点与焦点连起来）

4.定义+几何+辅助线+计算

我就算到这👆

接下来要用到计算

已知斜率K，翻译DE长度

要用到弦长公式（专门解决斜率问题，使用面也非常广）👇

这个式子还可以继续化简（因为一般我们都会与圆锥曲线联立）👇

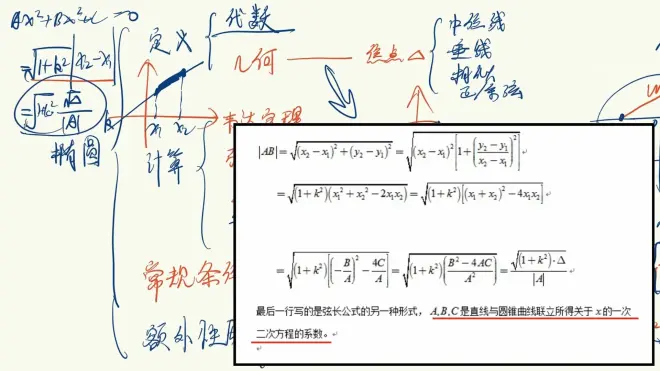
要学会给自己减少计算量👇

最终结果👇

Ⅱ.计算类

大致分为两种

简单一点的就是直接根据题目条件进行翻译

另外一种就是要用到一点特殊的方法

其中：

注意;韦达定理+弦长公式（非常高频！）

大部分时候的弦长都是根据弦长公式来求，哪怕K不已知也可以👇

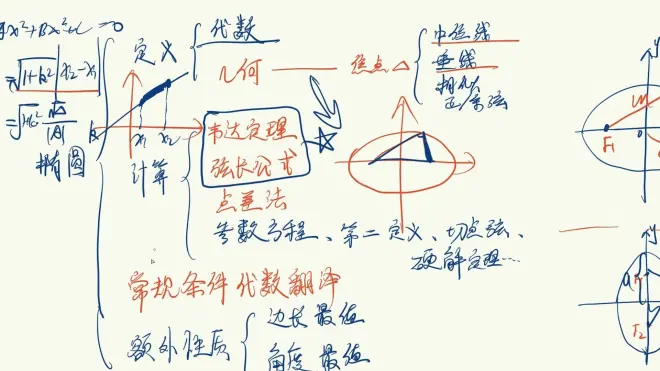
注意：点差法（只要是和弦中点有关的问题，都可以使用点差法）

适用？

题目给的直线和椭圆交于两点，如果题目问的问题或给的性质和这个弦中点C有关，基本都是采取点差法求解👇

考试的时候大题不能直接用，需推导

如👇

再如👇

除了上述两种特殊方法之外 （不常考）

参数方程：专门解决单动点问题

第二定义：解决焦半径，也就是焦点到椭圆上一点的长度

切点弦:解决含切线的问题

硬解定理:大题的运用

常规代数翻译题 就两个字：听话

如

椭圆其他额外性质

如 边长最值

其中，那个焦半径长=a🗡ex0的公式，后面会讲

如 角度最值 （推导过程看不懂）

例题