大人,时代变了!||Mathematica学习记录
//这是一篇关于Wolfram Mathematica的文章,主要记录软件学习过程中的一些困难与感想
//本文基于Mathematica 11.3编写。

摘要
本文记录了笔者学习Wolfram Mathematica软件的过程、遇到的困难与一些简单的应用。文章中简单记录了软件的基本使用方法、笔者在学习过程中的遇到的多种Bug,以及笔者在计算机基础等课程中对软件的应用。
1. 认识Mathematica
我首次见识Wolfram系列产品是在三年前,那时我还是个有梦想的物理竞赛菜鸟,而我遇到的第一个难题正是:微积分!(感谢当时的我在徐van♂强的"数学基础知识补充"下活了下来)经过几个月艰难的思考,刚刚勉强看懂定积分的我立刻又要面对一个更大的难题:如何求原函数!啥是三角换元?啥是分步积分?这玩意怎么算出来的?
这时候,同学手机里的Wolfram Alpha秀出了它的首杀!那是一个让我绞尽脑汁也算不出来的不定积分,记不太清但是它大概长这样...
同学默默打开了手机里的Wolfram Alpha,并输入原函数,然后我就看到...

连计算过程都能给我写出来!这是我第一次见到有软件能把不定积分这么困难的东西处理得这么完美!
再后来,高二暑假在厦大的苏国珍教授的竞赛课上,(教授真的讲得很好!)我再次感受到被Wolfram产品支配的恐惧。我还记得教授听到我们反映有的例题计算量太大算不出来时的回答:“这个你们算不出来吗?太难算了?我是用数学软件算的...” 没错这个数学软件,又是Mathematica...这两件事让Wolfram产品给我留下深刻的印象,于是来到大学有了自己的电脑后,我装上了这个软件,并打算让它像以前一样终结那些难题。
2. 基本操作与简单应用
当然,要让它发挥作用还没那么容易。毕竟Mathematica本质上是一种计算机语言,特别适合数学计算,但同样有局限性,同样有Bug。要用好它是需要时间的。好在我们学校的一本计算机教材里面有一些简单的教程,[1]以及这个软件自带了非常详细的帮助文档!

于是就开始照着案例学了起来。先来个简单的计算...

还算简单,只要注意调用函数用方括号,所有函数都需要首字母大写。
再来算一个极限...
这里就遇到了一个困难:这里的x→∞的“→”是怎么打出来的?看看书上的源代码:

再看看自己的键盘...没有右箭头啊?再后来,突发奇想:
(用减号和大于号组成的箭头也太抽象了吧!)
稍微熟悉一些函数之后,就来砍一道高数题练练手吧...[2]
听说有的不定积分很难?
不好意思,秒了

到这里我的大脑中一直回荡着的声音是:“大人,时代变了!”
3. 微分方程终结者
作为一个物院人,每天的日常之一,当然是微分方程:
有了Manthematica,人手能算的它几乎都能算...
不过,也并不是所有微分方程都能算出解析解,比如大角度单摆:
可以用NDSolve命令带上初始值数值求解,

也要记得把结果可视化,否则就只是一堆数字。定义函数存储前面的计算结果:
大家可能注意到这个First[]有点不好理解。这也是我遇到的最大困难,画图经常画不出来,后来向同学求教,知道了Mathematica的一个极为神奇的设定:大家可以看看前面的图六中的输出,输出结果外面带着两层括号!这也就意味着这里的y[t]/.s1或theta[t]/.s2被认为是数组,而直接用数组作为输入进行作图就会出Bug。所以用First提取了数组的第一个元素(唯一的元素)才终于解决了这个问题。计算成功的界面:

4. 大人,时代变了!
有了强大的软件,许多过去难以完成的计算现在变得可行了。我的计算机大作业就是《基于Mathematica求解混沌摆运动》;在力学大作业的理论分析里也利用到了Mathematica对微分方程的数值求解。
在计算机大作业中,我和物院同班一位同学主要负责的是物理建模和程序的测试(约等于绝大部分工作...)(是我高估了组里的数院人,真就从建模到微分方程再到软件使用都不懂啊)(不过选题也比较仓促,没有考虑到组内平均水平也是我大E了啊)那么以下简单描述一下理论模型:
两个质量为1kg, 长度为1m,粗细可以忽略的细棍首尾相接,并悬挂于固定点,所有连接均为光滑铰接。给定初始值,求解自由端的运动。我们直接采用分析力学求解。分两种情况讨论:
(1)摆动限制在一个竖直平面
如图,此时决定两个细棍位置的广义坐标只有α,β。

写下系统的势能:
以及动能:
然后就是万能的拉格朗日方程:
其中. 再给出合适的初值就可以用软件数值求解这些微分方程了。(当然这些微分方程组都没有解析解)
转换成代码:
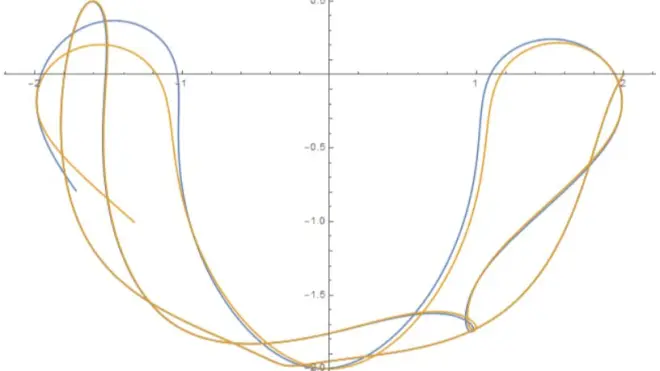
再画出自由端的轨迹:
结果如下...

甚至可以做出动画:
输出结果(计算量挺大的,耐心等待...)

(emm...B站投稿的文章好像放不了动图啊)
(2)摆动可以在球面内进行
我们取消之前设置的平面约束,这样的话每一根棍都需要两个广义坐标描述位置了,不妨设为
这理论就有点复杂了,需要我翻开我的理论力学[3]
简单来说,发生复杂变化的只有棍子的转动动能:
其中
是棍子垂直方向的角速度。而平动动能与重力势能形式和原来差不多,直接上代码:
然后,可视化输出:
就可以看到

还有...

然后最后大作业展示的时候我们上去一通瞎编,成功迷惑了助教和老师...现在计算机课还没出成绩,但愿这个大作业效果还可以...
而在力学大作业中,我们面对的问题是...分析小球在旋转平面上的轨迹...
If you put a light rolling object (e.g. a ring, a disc, or a sphere) on a horizontal rotating disc, it may start moving without being expelled from the disc. Explain how different types of motion depend on the relevant parameters.
事实上实验观察到的小球轨迹相当鬼畜...滚动摩擦不能忽略,这导致了决定小球运动的微分方程是非线性、无法求出解析解的:
此外这个微分方程的因变量是复数,本质上是两个常微分方程分别描述x,y方向的运动。这是由于我采用了一个常用小技巧:用复数表示平面上的位置,复因子作为矢量旋转因子,这个思路在之前求解傅科摆时也曾使用。

现在问题就在于这个带复数的微分方程还能用软件数值求解吗?
直接上代码试试:彳亍!

所以这是我学习过程中一个比较重要的发现:数值解微分方程是可以在复数域进行的。
总结
一个强大的模拟计算软件可以让一个物院人获得快乐,并极大降低了作业难度工作量,可以让我们更加合理地分配时间,把精力花在更有价值的问题上。但是,实际学习过程中我们也会发现,Mathematica仍然有一定局限性。
首先是算力有限,在一些特殊情况下软件求解的计算量会非常大,例如本文中提到的混沌摆,其实如果把前面贴出的代码全部走一遍是要好几分钟的。
其次有一些情况使用软件求解的算法可能无法正确处理一些不收敛的点,使得有时候软件需要很长时间才能给出结果,或者直接报错;在这些情况下手算技巧的重要性也就体现了出来。
所以,Mathematica不是万能的,它可以代替我们完成计算,但不能代替我们完成思考与理解的过程。我们需要合理利用,同时也保持一定的手算能力。
参考文献
[1] 赵宏 等. 大学计算机应用经典案例[M]. 北京:高等教育出版社,2020.8,101~113.
[2] 由同顺 等. 高等数学(上册)[M]. 天津:南开大学出版社,2016.9,199.
[3] 周衍柏. 理论力学教程(第二版)[M]. 北京:高等教育出版社,1985.9,281~287.

