【Aegisub】贝塞尔曲线偏移简单介绍、绘图(含曲线)转边框简单介绍

2022-05-02 17:59 作者:多华宫与火火里 0人读过 | 我要投稿

之前讲过如何将全直线绘图转边框(以及断裂边框、自定义起点终点的转边框)，后面还讲过得到简化的全直线边框(即没有路径自交也没有多余路径)，但是直接将带有曲线路径的绘图转边框也是有意义的，比如文本量更小、看起来可能更光滑之类的。

一般来说，一条三阶贝塞尔曲线的等距偏移曲线不会是一条三阶贝塞尔曲线

有的三阶贝塞尔曲线是可以直接把它的控制多边形顶点给等距偏移，然后得到它近似的偏移曲线的，比如图1.01的曲线得到图1.02的边框

图1.01的绘图代码是m 0 0 b 10 -8 32 -10 50 -5

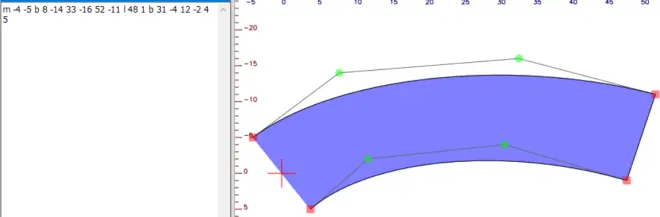
图1.02的绘图代码是m -4 -5 b 8 -14 33 -16 52 -11 l 48 1 b 31 -4 12 -2 4 5

放在一起看，得到了图1.03

其实基本上来说，此时就仅仅是把原本曲线的控制多边形顶点给等距偏移了，然后就得到了相应的偏移曲线，如图1.04

可是，当你曲线有曲率很大的点时就不能这样做，当你设定的偏移值比你曲线某点的曲率半径要大的时候，直接偏移曲线的控制多边形顶点是得不到比较理想的曲线的，如图1.05

偏移得到图1.06，放一起就是图1.07

显然，虽然控制多边形的顶点是等距偏移的，但是得到的曲线却不是等距的。这就是因为原本曲线在比如 t 处的曲率半径比偏移数值小了，如图1.08

众所周知，曲线在某处看起来越弯曲，那么这点的曲率就越大、曲率半径就越小；曲线在某处看起来越平，那么这里的曲率就小、曲率半径就越大(因为曲率半径是曲率分之一)。显然，一般的曲线每点的曲率是不一样的(圆的每一点的曲率都一样，且曲率半径就是圆的半径)。那么你想想看，比如你希望曲线偏移6，但是你曲线上某点的曲率半径是2，那你直接偏移控制多边形的顶点很尴尬吧？

正如一开始说的，一般的三阶贝塞尔曲线的偏移曲线根本不是三阶贝塞尔曲线，所以你想用区区一条曲线就表示原本曲线的偏移曲线是不可能的。所以什么意思呢，就是说，三阶贝塞尔曲线的偏移曲线(经常)需要由多条三阶贝塞尔曲线构成。也就是，将原本的曲线拆分为多条曲线，然后偏移这一条条的曲线即可。

关于三阶贝塞尔曲线的偏移，我参考了一个js写的bezier库以及c++写的qt库。用js的那个库叫啥忘了，但是它用的方法我觉得不算太好，它有求一阶导二阶导，然后甚至从开始一点点的检查曲线上的点(从0.01到0.99、每次加0.01好像是)，用这种方法拆分曲线，计算量总之不算特别小、而且拆出来的曲线条数比较多，而qt库呢它使用的方法就计算量小不少、且拆出来的曲线条数一般比较少，我大概根据qt库的算法写了一个贝塞尔曲线偏移的代码(不完全一样)

另外，qt库的转边框在某些时候会有奇怪的错误，它的端点会添加错误，当然我自己写就至少可以避免这种错误。如图1.09是原本的曲线，qt库(A3shape)转边框得到图1.10

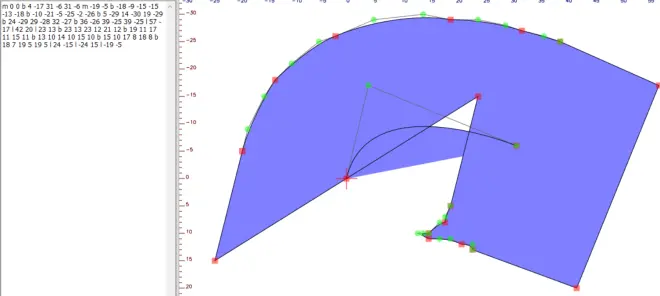
用我自己写的转边框就会得到图1.11

然后简单介绍一下三阶贝塞尔曲线偏移的算法，粗略介绍一下，反正我知道这些东西压根没几人会看并且看完的（有不知道有Yutils教程的,我记得我两年多以前就出了Yutils的视频，讲了常用的那些函数怎么用以后，我就开始教的如何自己写插件自己写函数库，也没几人看没几人知道），不想学多简单，那我少讲点

首先，一条曲线设定最多拆分为16条曲线，用一次次的递归来拆分曲线，当然并不是所有的情况下都要拆分曲线的，有的不需要拆分。所以对于一条曲线A，先偏移它的控制多边形顶点，得到新的曲线B，检查 t 为0.25、0.5、0.75时的情况，比如检查在 t 时，A曲线上的这一点和B曲线上的这一点的距离和你设定的偏移值的相差大不大之类的，如果满足一定条件，就在相应的 t 处将曲线拆分，然后同样的，拆分出的曲线也要一样的检查，比如 t 在0.25、0.5、0.75时的情况，然后看拆分不拆分之类的，也就是递归嘛，这样下去，但是要设定原本的曲线最多被拆为16条曲线，就是说递归拆分曲线，如果已经拆出了16条，那么就不会继续不停地递归了。还有就是添加圆弧，就是有的时候偏移数值太大，那么偏移曲线就会加相应的圆弧，比如你曲线的边界框bbox高宽不超过10、但是你希望这个曲线偏移23333，那你这个偏移值也太大了吧，此时就会做圆弧了，比如图1.12这样一条曲线

图1.12的绘图代码为m 0 0 b 2 0 2 -1 1 1

显然，这曲线非常小，但是你要忍一下。现在转边框、让偏移值为210，就得到图1.13

偏移值很大，你要忍一下

显然，偏移值太大的时候，就会做圆弧了，比如可以设定曲线的bbox的宽高都小于偏移值的0.1时，判断一下需不需要加圆弧，如果满足相应的条件就加、不满足就不加

然后，一条曲线就可以偏移了，那么转边框当然就是要得到两条(组)偏移曲线了(原本曲线两侧各需要一组偏移曲线)，比如图1.14的曲线转边框得到图1.15(图1.15里含有原本曲线,方便观察)

显然，原本的曲线就被拆为了几段，然后这几段就分别偏移它们的控制多边形顶点，然后就有了相应的偏移曲线了，当然现在这里转边框是加了端点的，不加端点就会得到图1.16

当然不加端点也是正确的偏移，只是作为转边框来说，至少加上端点会好看些。那么你也设定端点样式是圆的，如图1.17

那么你知道了三阶贝塞尔曲线怎么得到偏移曲线后，不就可以写绘图转边框了吗？之前讲过线段怎么偏移的，比如图1.18的线段AB

假设A点坐标(x1,y1)、B坐标(x2,y2)，那么线段AB可以求出个法向量(y2-y1,x1-x2)，然后再把这个法向量变成单位向量，假设求出的单位向量是(ux,uy)、假设你要偏移的数值的d，那么你就可以得到偏移的线段的顶点了，偏移的线段第一个点x坐标就是x1+ux*d、y坐标就是y1+uy*d，然后当然偏移的线段第二个点x坐标就是x2+ux*d、y坐标就是y2+uy*d

这样不管是直的还是弯的，都可以偏移了，转边框不就可以很简单的写出来了吗，这样比如图1.19就可以转边框得到图1.20了

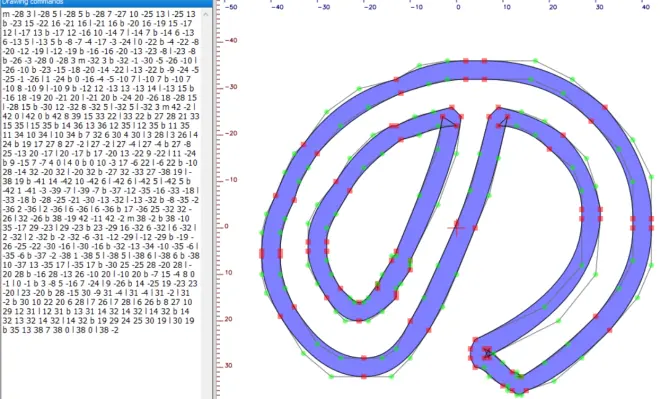
而如果用先把绘图转直线再转边框的方法，那文本量就会比较大了，如图1.21

那么此时你可能就会想，既然先转直线再转边框会有这么多文本，那么岂不是全直线转边框的函数没有用处？当然不是这样的，直线绘图转边框是有用的、相较于含曲线路径的转边框有它的好处，那就是，当你希望做变形效果的时候，比如你得到了边框绘图，你对它做变形效果、改变绘图的顶点，那么当然用全直线的边框就会好一些，而含曲线路径的边框就有一些"多余"的路径，相当于一个未简化的绘图，变形起来的时候还会有多余的点、干扰效果，那自然是不好的。而之前介绍过，如何得到简化的全直线边框，那对一个没有多余路径的绘图来变形的话，就会舒服很多。所以说，直线边框和有曲线的边框都有它们的用处，只不过一般来说，不会做变形效果，所以一般用曲线绘图转边框的函数即可、那样文本量就会小一些。

另外再提一下转角样式是什么意思。如图1.22这样一个路径，比如现在要在一侧得到偏移路径，那么就会得到图1.23吧

那么显然每个片段偏移以后，并不算直接连接上的，如图1.24，所以对于有很多段路径片段的一个绘图来说，路径片段与路径片段偏移后就需要将各自偏移后的片段连接上，而这个连接的方式就叫做转角样式

如果直接连接的话，这种样式可以叫做bevel，如图1.25就是bevel

如果是用一段圆弧连接的话，这种样式就叫做round，如图1.26

如果愿意延长求交点的话，那么就是miter样式了，如图1.27

所以很显然，这几种转角样式里，计算量最小的是第一种，因为根本不需要计算，直接连接即可。什么意思，连接不就是 l 命令吗，绘图代码里直接用' l '把一段段偏移后的路径连起来就完了。然后其它比如round就是算一下相应的圆弧即可，三阶贝塞尔曲线拟合圆弧很简单。然后miter模式要算交点，但是有的时候因为转角太小，导致直接用交点会很难看，比如图1.28

应该看得很清楚吧？黑色是原本的路径，两个线段的夹角太小，这样直接求交点就会有很长一段尖尖，所以miter样式一般不会直接这么求交点，而是，比如你偏移数值是10，那么就延长嘛，都延长10，如果有延长了这个10(即路径的偏移值)后，有交点，那么就用，如果没有交点，就直接连接了，如图1.29，假设偏移值就是10，然后延长