用导数的定义求极限(limit)_AP 微积分
DEFINITION OF DERIVATIVE ( 导数的定义)
The fraction is called the difference quotient for
at
and represents the average rate of change (ARC) of
from a to a + h.
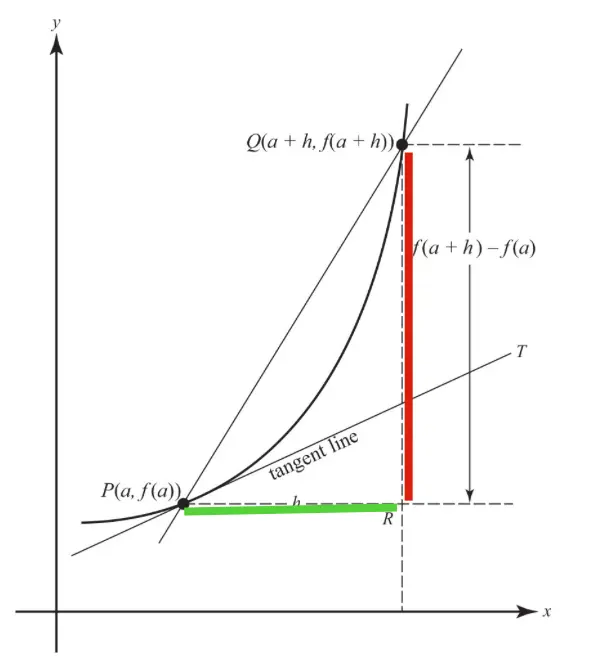
Geometrically, it is the slope of the secant PQ to the curve y = f(x) through the points P(a, f(a)) and Q(a + h, f(a + h)). The limit, f′(a), of the difference quotient is the (instantaneous) rate of change of f at point a. Geometrically (see Figure 3–1a), the derivative f′(a) is the limit of the slope of secant PQ as Q approaches P—that is, as h approaches zero. This limit is the slope of the curve at P. The tangent to the curve at P is the line through P with this slope.
在几何学上,它是通过点P(a, f(a))和Q(a+h, f(a+h))的曲线y=f(x)的割线PQ的斜率。 差商的极限f′(a)是在a点的(瞬时)变化率。这个极限就是曲线在P点的斜率,曲线在P点的切线就是通过P点的斜率的直线。

key
35. ,
,
;key
36. ,
,
; key
37. ;key
38. ,
,
; key

