基于非线性模型预测控制的无人机路径规划
一、研究背景
无人机在在众多的应用领域展示了其良好的能力,如基础设施检查、地下矿井导航、搜索和救援任务、在事故发生时提供急救或除颤器等。然而,在进行这些任务时需要考虑到环境的因素如狭窄的通道、有限的入口面积和一般狭窄的受限空间,以及限制可用开放空间的多种障碍物。有时还应该考虑移动障碍物的情况下。更具体地说,要在复杂的任务中部署无人机,如城市环境、非结构化和未知或不断变化的应用场景,例如存在多个移动障碍物和其他机器人代理,必须保证安全操作和与居民的零事故。因此,应用一种新颖的非线性模型预测控制(NMPC),以建立一个在受限环境中的完全自主导航框架非常有意义。
非线性模型的应用在无人机路径规划中具有广泛的应用前景,因为它可以更好地模拟无人机飞行的复杂动态特性,以及考虑更多的控制因素。在非线性模型中,可以考虑无人机的飞行速度、空气动力学力学特性、环境参数、传感器测量误差等因素,从而提高无人机路径规划的精度和鲁棒性。而且预测控制是一种常用的非线性控制方法,它可以通过对未来状态的预测来调整当前的控制策略,从而提高系统的控制性能。基于预测控制的无人机路径规划方法可以通过对未来的无人机运动进行预测,来优化无人机的轨迹规划,使其更加符合实际应用场景。此外,基于预测控制的无人机路径规划方法还具有适应性强、鲁棒性好等优点。
二、针对动态障碍物
大多数研究是针对动态或移动障碍物的情况进行的运动规划,主要是在自动驾驶汽车的背景下,因为它需要确保城市环境中的无碰撞路径。如果解决了计算时间的问题,NMPC的运动规划方法也开始在无人机领域获得更多的应用。与其他避障方案相比,NMPC方案的优势在于能够纯粹基于无人机的非线性运动学产生无碰撞轨迹,其中轨迹中的每一点都由一系列控制输入描述。其主要问题是求解时间。参考相应文献,对于动态避障的做法是通过对障碍物轨迹进行预测,输入到系统作为控制器的参考,然后MPC控制器可以根据预测模型和当前状态,计算出最优的控制输出,以达到运动规划和避障的目的。优化是通过非线性、非凸的求解器Proximal Averaged Newton for Optimal Control(PANOC)及其相关软件OpEn(优化引擎),其中应用了一种惩罚方法来适当考虑导航过程中的障碍和其他约束。具体方法可以分为以下5个步骤。

(1)无人机运动学:根据机体坐标系和全球坐标系,将无人机的6个自由度由状态方程组定义:

其中p为xyz位置,v为线速度,φ和θ∈[ - π , π]分别为沿xW和yW轴的横滚角和俯仰角,R ( φ ( t ),θ ( t ) )∈SO ( 3 )是描述姿态的欧拉形式的旋转矩阵。φref∈R,θref∈R和T≥0分别是横滚、俯仰和总推力的参考输入。线性阻尼项Ax,Ay,Az∈R和重力加速度g。将姿态项建模为姿态(横滚/俯仰)与参考φ ref∈R,θref∈R之间的一阶系统,其增益为K φ,Kθ∈R,时间常数为τ φ,τ θ∈R。

(2)定义成本函数
用x =[p,v,φ,θ]的转置表示状态向量,用u =[T,φref,θref]的转置表示相应的控制动作。对采样时间为δt∈Z +的每个时刻(k + j | k)采用向前欧拉法离散化式。其中(k + j | k)表示第k + j个时间步的预测,产生于第k个时间步。这个离散模型被用作NMPC的预测模型。用xk和uk表示完整的预测状态和相应的控制输入,沿着预测水平线相应地表示,控制器的目标是使状态达到规定的设定点并提供平滑的控制输入。所以,成本函数表述为:

其中Qx,Qu,QΔu分别是状态、输入、和输入变化率的正定权重矩阵,第一项表示状态成本,它惩罚偏离某个状态参考xref的行为。第二项表示输入成本,惩罚偏离稳态输入uref=[g, 0, 0]的行为。第三个项,对连续输入的变化进行惩罚,来保证执行平滑的控制动作。
(3)定义障碍和约束
使用函数[h]+ =max{0,h}。这使我们可以将约束条件表述为等价表达式,如[h]+=0意味着约束条件得到满足。通过选择h作为一个在约束区域内为正值、在约束区域外为负值的表达式,[h]+将在约束区域内为正值,在约束区域外为零。障碍物的约束被定义为:

其中ξobs =[robs,rs,pobs x ,pobs y ,pobs z],robs是障碍物的半径,rs是额外的安全半径。这意味着,只要无人机的位置p位于球体之外,上式就为零,可以说是一个平等的约束条件。将这扩展到动态障碍物上,为每个预测的时间步骤形成一个单独的约束。让pobs x , pobs y , pobs z表示描述障碍物轨迹的大小为N的向量,rs表示沿N线性增加的安全半径,pk表示在时间步骤k的全部预测的无人机位置,那么障碍物约束向量可以表述为:

如果无人机没有进入障碍物轨迹所描述的球形障碍物,则满足约束条件。此外,为了避免快速移出障碍物的轨迹会导致控制输入的激进或振荡行为,因此为控制输入φ ref和θ ref的变化幅度设定一个上界和下界:

最后,还应该对控制输入施加约束,定义输入边界:

(4)进行优化
综合考虑上述的成本函数和相应的约束,可以将有N个球形障碍物的参数化轨迹的NMPC问题表述为:
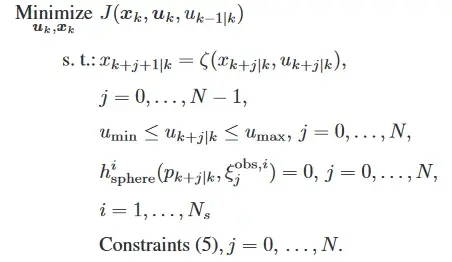
采用PANOC这种优化器和相关的Open开源软件进行优化,找到一条移动成本最小值,而且不违反约束条件,或者说直到满足一个特定的容忍度的轨迹。
(5)轨迹的分类
在进行障碍物移动轨迹预测时,将其轨迹分为三类:直线运动、弹丸运动或静态障碍物。因此,在可以计算障碍物轨迹类别的情况下,可以使用直接预测模型来预测障碍物的未来位置。直线运动描述为:

其中vobs是障碍物的速度,没有力作用在障碍物上。弹丸运动轨迹定义为:

其中B是线性空气动力阻尼项,通过前向欧拉离散化,使用与控制器和预测模型相同的采样时间Ts。对于障碍物状态xobs = [pobs,vobs],离散预测的形式:

其中αt表示轨迹的离散预测模型,可以无限期地迭代。同时与先前测量的障碍物位置和速度的矢量做比较测量误差为:

对3类不同的轨迹进行评价,选择误差最小的一类进行轨迹预测。部分仿真结果如下图:

三、针对静态障碍物(狭缝、窄口等)
无人机在狭窄的通道、多障碍物填充的空间和狭小的开口等约束环境中的路径规划同样采用NMPC的方法,通过增加惩罚约束,并采用PANOC的优化方法最终计算一条不进入障碍物的路径。这种方法的研究步骤与移动障碍物的相似,其中无人机运动学采用上述第二节描述的一样,成本函数也与上述第二节描述的一样,因为目标一样获得一条平滑且避开障碍物的一条轨迹。
(1)障碍物定义与约束
函数的定义与上述相同,将周围环境中可能会遇到多种不同类型的障碍物分为三种类型:圆柱体形状、多角形表面和受约束的入口或通道。应该强调的是,所有的基本约束都是在控制范围N上加起来的,以考虑到所有预测的未来时间步骤的障碍物约束。①圆柱体形状障碍:该约束条件可用于任何受阻区域或一般障碍物,其中圆柱体的半径笼罩着不希望出现的区域。因此,其约束定义如下:

其中xobs、yobs、zobs和robs分别为障碍物的x、y、z坐标和半径。将这两个方程相乘得到约束方程:

障碍物可视化如下图所示

②表面型障碍物:表面障碍物用六条线或平面方程表示一个有限定宽度、长度和高度的墙状障碍物。为了便于表述,一维线或平面情况可以用沿每个轴的最小、最大范围表示为:

其中p表示无人机的位置坐标,pmin,pmax表示约束区域的范围。设x,y,z的每一个h项分别描述一个线/面方程,则全曲面为:

在不失一般性的情况下,该框架可以直接扩展为全平面方程来描述障碍物表面,其可视化如下图所示:

③限制性出入口:首先可以由y-z平面上的圆柱体形状来描述,那么其圆柱形状的约束表达式为:

然后为了限制通道面积的大小,定义了x方向上的通道长度的约束条件:

其中xobs、l1、l2分别是通道的中心和x方向上的通道范围。与以前的情况一样,约束在预测时域上加总:

可视化如下图所示:

(2)控制输入约束:为了确保即使在非常苛刻的避障场景下,控制输入φ ref和θ ref的非激进行为,可以表示为:

这些约束将控制输入从一个时间步到下一个时间步的变化限制在一个最大值,这里分别记为Δ φ max和Δ θ max。除速率约束外,令控制输入的硬约束记为:

(3)优化:优化引擎可以使用二次惩罚方法求解参数优化问题,其核心是非线性非凸求解器PANOC:

其中f是一个Lipschitz微分函数,F是一个矢量值映射,c是一个正的惩罚参数。将上述描述的成本函数、约束条件通过单射来适应这个框架,并设置Z为(11)式的约束。此外让F映射出障碍物和输入率的平等约束。参数p包括状态向量X的初始条件,以及参考和障碍物数据。圆柱形、多边平面、限制性出入口障碍物仿真结果如下图所示:
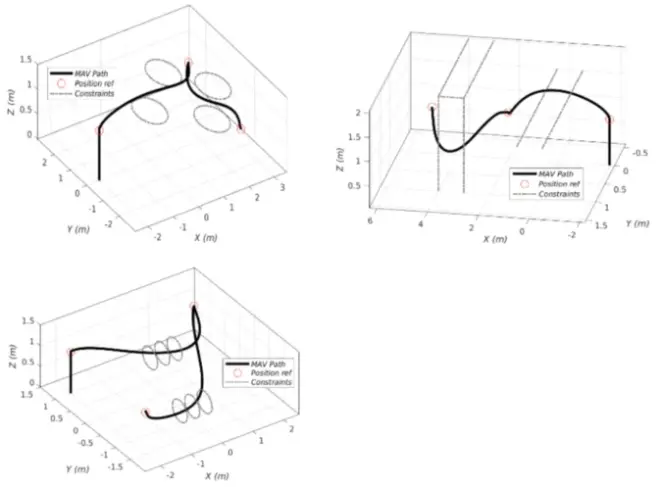
四、分析与思考
①对于移动障碍物轨迹将其分为三类,未考虑其他类型的轨迹运动,比较局限。因此,可以通过对事物或人或其他一些移动障碍物的轨迹可以进行一个深度学习,然后发现其运动的规律,更好的预测其行为轨迹,达到更广的适应性而且也可以更好避障。
②上述提到避开移动障碍物的方法未考虑到障碍物移动速度的因素,如果障碍物以一个较快的速度飞向无人机,无人机通过上述方法可能无法闪避。因为其计算的时间以及机体整个按规划的路径移动需要时间。因此,如果对机体姿态的调整,通过细化机体本身大小与移动障碍物大小,增加距离约束和可避开半径约束的,调整控制横滚和偏航角的大小来避开移动障碍物,姿态调整一方面减少所需时间,另外一方面对与路径规划其偏离参考轨迹范围小,保证路径渐进最优。
③通过NMPC对静态障碍物的避障,对障碍物形状描述还是比较局限,而且通过仿真发现其规划的路径并不是最优。与路径规划算法(RRT*等)和轨迹优化算法比较起来,这种方法优点:计算量小,效率高因为其不需前端和后端两个规划器。但是得到轨迹平滑性相对差一点,且路径长度相对与其他算法较长。
④在使用滚动优化时,对于局部目标的设定非常重要,设置合理,对于无人机飞行时轨迹遵循较好,不会过激的通过目标位置。
五、参考文献
[1].Lindqvist B, Mansouri S S, Agha-mohammadi A, et al. Nonlinear MPC for collision avoidance and control of UAVs with dynamic obstacles[J]. IEEE robotics and automation letters, 2020, 5(4): 6001-6008.
[2].Lindqvist B, Mansouri S S, Nikolakopoulos G. Non-linear mpc based navigation for micro aerial vehicles in constrained environments[C]//2020 European Control Conference (ECC). IEEE, 2020: 837-842.

