有意思的概率与统计(二)
概率论的坑,要开就得开得迅速和有力!
所以很快啊,我又来更新第二篇了!
上一次介绍了随机现象及其相关的各种概念,为我们本次继续介绍概率提供了足够的基础。
于是乎,这一次,我们直接来介绍——
Chapter One 随机事件与概率
1.2 概率的定义及其确定方法
概率论,顾名思义,所研究的问题主要集中于“概率”二字之上。所以,我们首先就有必要弄清楚,什么是概率。
我们对概率都有一个直观的认识,因为我们在日常生活当中经常听见各种有关概率的说法:
(1)买一张彩票中一等奖的概率小于0.003;
(2)明天降雨的概率大于80%;
(3)投掷一枚质地均匀的硬币,正面向上的概率为1/2。
这样的例子有很多,其中所涉及到的“概率”的具体确定方法和所表达的意义都不尽相同。比如说,第一个说法当中,虽然没有概率的确数,但是这个结果却是基于大量的事实结果和实际彩票的发行情况估计出来的,具有准确的参考价值;但是对于第二种情况来说,这个概率只是人们(或者是专家)根据自己的经验和掌握的规律做出的一种主观推测,并不是概率的真实值,称为主观概率(很多时候,虽然是主观概率,但也不失为一种确定概率的方法,日常中用于描述问题结果已经足够了);而第三种描述当中,由于我们十分明确抛掷硬币的结果,所以我们也很容易就给出一个理想的概率值,这个值是较为准确的。
但无论如何,概率都有一种被人们所公认的含义——事件发生的可能性的度量。
但是,这样的含义显然不能够将概率变为一个精确的数学对象供我们研究。因此,我们需要一个有关概率的一个严格的数学定义。经过数学家们的不断尝试,目前较为公认的是1933年由数学家Kolmogorov提出的以下公理化定义(感兴趣的小伙伴们也可以了解一下其他的定义):
设为一样本空间,
为
的某些子集构成的一个事件域。如果对任意事件
,定义在
的一个实值函数
满足:
(1)非负性:;
(2)正则性:;
(3)可列可加性:
若,则
则称为事件A的概率,称
为概率空间。
这个定义完美符合了人们对概率的认识,比如说,概率不会为负数,概率应该对应事件等等。另外,这样的定义给出的概率是十分严格而准确的,作为一个数学对象来说,是十分利于我们研究的。
这个定义中最重要的一点是,它表明了概率是集合(事件)的函数(或许我们可以称之为泛函也说不定,不过这都是后话)。
虽然我们已经有了明确的定义,但是在如何确定概率这一方面仍然没有明确的方法。主要原因就是,概率本身和事件高度相关,而某一事件发生的可能性仅凭这样的定义是没法完全说明的。我们需要引入一些基本假设,才能够基于这些假设给出事件的概率。
举个例子,我们都知道,投掷一枚骰子,事件“点数为奇数”的概率为0.5。虽然这样的概率让人信服,并且它也满足了公理化定义,但我们仍未可知这样的概率到底是怎样得出来的,到底与事件本身有怎样的关系。所以,接下来,我们就要介绍一些确定概率的方法。
一个经典的方法,就是——以频率估计概率。
这个方法的思想核心是,在大量的重复试验当中,属于待确定概率的事件A的结果出现的频率(频数与总次数的比值)是会几乎稳定在某一个常数附近的。这一方法的总过程大致如下:
(1)与考察事件A有关的随机试验可以大量重复进行;
(2)记n(A)为事件A在n次试验中出现的次数,称为事件A发生的频数,数字:
称为事件A发生的频率;
(3)随着n的增大,事件A的频率会更加倾向于稳定在常数a附近,这个数值称为频率的稳定值。以频率估计概率时,通常认为此稳定值就可以代表概率。
这样的方法有它的好处,比如说得出的概率值十分令人信服,也可以作为日后再次进行类似的试验时对结果的预测依据。但是,其缺点也是十分明显的。很多时候,我们没办法将试验大量重复,因此也就没有办法通过这样的方法获得概率值。
既然如此,我们就需要一些偏向于理论逻辑导出的方法。首先要研究的,就是古典概型。
所谓古典概型,就是确定概率的最为古老经典的方法。这一方法是概率论历史上最先开始研究的情形。这样的方法简单直观,也避免了做大量的重复试验。只需要一些理论逻辑分析,我们就可以轻松得出合理的概率值。
这一方法的思想核心是一个基本假设——等概率假设。
设若样本空间是一个有限集,且各个样本点发生的可能性是相等的。这样,我们就可以认为,每个样本点自己构成的子集(事件)的概率都是均等的。此时,某一事件的概率就等于事件当中所包含的样本点的个数。也即:
在一些问题当中,我们会涉及到一些几何模型。事件的描述很多时候能够通过几何规划的方式来表示出来,这个时候,我们就可以通过一些几何度量来作为事件可能性的代表,以此来求出事件的概率。这就是几何概型。
如果一个随机现象的样本空间充满某个区域,其度量可以用
来表示。而事件A是所代表的区域是
中的子区域,那么该事件的概率就为
。这个概率称为几何概率。
值得注意的是,几何概率很多时候和我们所选取的几何度量相关。有一些现象表明,对于同样的时间而言,选用不同的几何度量所求出的几何概率并不相同。究其原因,可能是不同的几何度量所对应的几何维度的划分方式有所不同,进而导致样本空间以及事件所代表的区域产生了差异。也就是说,对于复杂的问题,“等可能性”这一说法太过于模糊,这样简单的假设反而会招致麻烦。(一个经典的例子就是Bertrand奇论。)
至此,我们就将所有确定概率的方法介绍完了。但是,尽管方法十分简单,可在应用的过程当中却演变出了许多经典的模型。在实际问题当中,多数情况都逃不出这些经典模型,因此还是有必要将其细致地介绍给大家~
我们先从最简单的抛硬币入手,让大家进一步理解一下等概率假设。
例1:现在,我们抛掷两枚完全相同的硬币,求事件A=“出现两个正面”的概率。
样本空间为:
事件
于是概率就为1/4。
这个例子似乎很简单,没什么值得深究的。但是,很多人会认为样本空间为:
这样似乎概率就应该是1/3。但事实上,虽然两个硬币完全相同,不加区分,但是我们总是要选择一个硬币先描述它的结果,然后再分析另一个硬币的结果。这样,我们就人为地给两个硬币附加上了合理的序号,导致了“一正一反”这个结果包含了了两个样本点。在这里,所谓不加区分,实际上是不区分两个硬币谁为1号,谁为2号罢了。
所以,想要使用等概率假设,重点在于要保证每一个样本点本身确实只含一个样本点。
接下来,我们就要研究一些基本的模型了。
例2:(抽样模型:不放回抽样)
一个盒子里装有N个球,其中有M个红球(n≤N),其余都是白球。现在要从中取出n个球,试求事件A=“取出的球中有m个红球”的概率。(m≤M,n-m≤N-M)
不难想见,样本空间中的样本点数应为。我们主要来研究的,就是事件A包含了多少的样本点。
事实上,我们可以将抽取过程分为两步,一部是先在红球堆中抽出m个,然后在白球堆中抽出n-m个。这样,在此理解下,事件A所包含的样本点数就为。
此时,事件A的概率就为:
若将m看做是随机变量,则根据m的取值不同,我们能够得到不同的概率值。由于各情况必有一种会发生,所以概率总和为应该为1。
我们将随机变量与其对应的概率值列成一个表,类似如下:

这称之为一个概率分布。
例3:(抽样模型:放回抽样)
我们刚刚介绍的例子,是不放回抽样的典型例子。接下来我们要讨论的,就是放回抽样的特点。所谓放回抽样,顾名思义,其实就是在每次抽取之后,我们将所抽取的样本再次放回样品堆中,不改变样品堆内的样品组成。这样,每次抽取时,同一事件发生的概率是不会改变的。
比如说,同样是刚才的情景,我们现在改成每一次抽取一个球,抽取后将其放回盒子中,现在求解事件B=“一共抽取n次后,抽到过m次红球”的概率。
一共抽取n次后,由于每次盒子中都有N个球,所以样本点总数为。
同样的道理,每次抽取球时,红球和白球的数目是不会变的,所以每次抽到红球,都是在M个红球当中抽出来一个。这样,我们只要选择,到底是第几次抽出红球即可。
于是,我们能够推知,事件B的样本点数为:
这样,我们就得到:
例4:(信箱模型)
在过去科技并不发达的时代,人们联络的主要方式是信件往来。因此,邮局便在其中起到了很重要的作用。
寄信并不麻烦,只需要将信息都填好,封存好,再贴上邮票,投入信箱就可以等待邮递员收走并发往各地。
陆逵同学很喜欢写信,因此他也常常寄信。在他家附近一共有N个信箱,他每次差不多都要寄出n封信。这些信都是写给他的好朋友们的。现在他想知道,这些信分别被投进不同的信箱的概率是多少?
这个问题倒是不难,首先需要解决的点是,样本空间中的样本点总数是多少?
因为每次一共有n封信要寄出,就有n封信要投递。每封信投进无论哪个信箱其实都能够被寄出去。而信箱本身是可以容纳很多封信的,因此也不必担心有的信箱投不进信的情况出现。
这样的话,每一封信都有可能投进任何一个信箱当中。于是,样本点的总数就应该是。
现在我们要考虑,这n封信分开被投进n个信箱这一事件(记为事件A)的样本点数是多少。
如果不加限制,只需要投进任意n个不同的信箱中,一个箱里面放一封即可的话。那么,首先,我们就要选出n个不同的信箱出来;其次,我们再将这n封信一封一封地投入这些信箱当中。所以,样本点数就为:
于是概率就为:
如果我们对这n个信箱有要求,必须是我们给定的某几个,那么这个时候,我们就没有必要去选择信箱了,因此组合数也就不会出现在概率表达式当中了。
这个模型虽然是来自于基本的生活内容,但是实际上,在统计物理当中,这个模型起到了至关重要的作用。在统计物理当中非常重要的三种统计——Maxwell-Boltamann统计,Bose-Einstein统计和Fermi-Dirac统计——就是基于这样的模型推导出的。
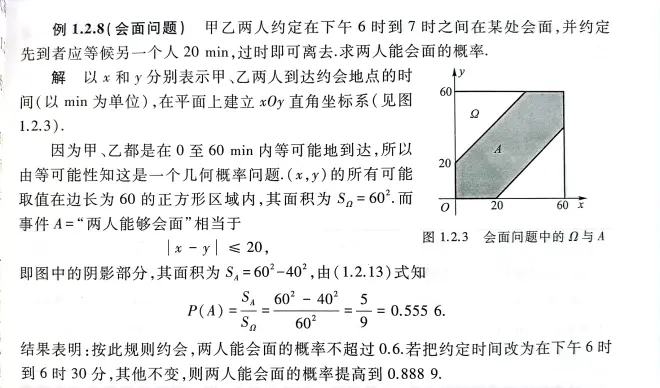
例5:(会面问题)
这是个几何概型的应用。篇幅关系直接展示给大家即可,理解其中精髓并不困难。
最后,我们来介绍一个十分有用的方法——随机模拟法。
随机模拟法,又称Monte Carlo方法,是一种通过大量重复所设计的模拟随机试验,来获得某种想要的数值的近似解的方法。通过提高随机试验的次数,进而提高近似解的精度。
这种方法的巧妙之处在于,只要设计一个随机试验,使得某一事件的概率与想要求解的参数相关,这样就可以通过以频率估计概率的方式,近似得出概率值。再通过其与理论值对比,进而求出参数的近似解。
一个经典的例子,就是投针问题:


思考:
证明以下组合数公式:
(1)
(2)
(3)
求以下事件的概率:
(1)抛掷三枚硬币,出现至少一个正面;
(2)任取两个正整数,它们的和为偶数;
(3)把10本书任意地摆放,指定的4本书放在一起;
(4)n个人随机地围一圆桌而坐,指定的甲乙两人坐在一起;
(5)把n个“0”和n个“1”随机地排列,没有两个“1”连在一起;
(6)在区间(0,1)中随机取两个数,两数之和小于5/7;
从一副54张的扑克牌(包含大小王)当中任意抽取4张,求下列事件的概率:
(1)全是黑桃;
(2)同花;
(3)同色;
设10件产品中有2件不合格品,从中任取4件,设其中不合格品数为X,求X的概率分布;
将三个球随机地放入4个盒子中,求盒子中球的最大个数X的概率分布。
最後の最後に、ありがとうございました!

