MC 非作弊情况下依靠C语言辅助建造圆形

        声明：本人只是一个中考完的初中生。本文介绍的方法应该与其他人的方法类似。如有不同方法，欢迎学术讨论。C语言是初二自学的，现在忘得差不多了。有错请纠正。请勿居高临下地指指点点。

        我们知道，MC中的坐标是以方块为单位的整数坐标（玩家位移时的坐标会有小数存在，本文忽略不计）。那么，如何在整数坐标中近似地画出一个连续不离散的圆？

        可以将MC的坐标看作平面直角坐标系，每一个方块就是坐标系上的点。那么，只需要算出圆上所有整数点的坐标就能够在MC中画出一个圆。

        圆的隐函数可以写作（有错请纠正），如果圆心坐标知道，设为（a,b），那么此圆可写作.这种方程我们初中并没有学过如何解，但是我们可以从中得出，圆可以分成无数个以圆心为一顶点，平行于x轴的线段、平行于y轴的线段为直角边的直角三角形。据此，只需要解这个三角形，即可算出来圆上任意点的坐标。三角函数的进阶计算我们初中还没有学，于是我使用电脑辅助计算。以下开始施法

        先上一张图（几何画板不会用）

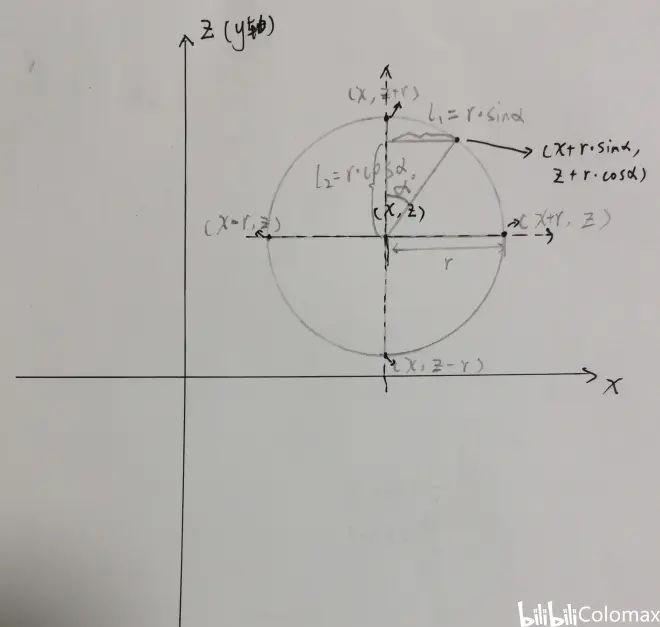
        以MC中的x,z为坐标轴，任意坐标为原点建立如图的平面直角坐标系。之后任意画一个圆，圆心坐标为（x,z）。可以看出，圆上坐标表达方式有四种，那么把圆再分成四个象限。第一象限内点坐标（）

第二象限内点坐标（）

第三象限内点坐标（）

第四象限内点坐标（）

        由于我用到三角函数，那么角度是必须的。我的思路是，从=0开始，不断迭代一定的角度，算出来的数值，之后进行四舍五入取整。这里用四舍五入取整并没有经过严谨的证明，可能有其他取整方式，欢迎讨论（大概率我听不懂）。

        有了这些数据，就可以开始写程序了。我此处用的是C语言，编译器为CFree。每次迭代的角度度数为1度。对于半径较小的圆来说，这种精度足够了。但是对于半径大的圆，就不够精确了。后续再讲。

        有点长，里面涉及到的一些算法我有时间再写专栏解释（挖坑.jpg）。运行结果如下：

        此程序的精度取决于每次迭代的角度增量。在C语言中，计算三角函数首先要包含一个<math.h>头文件，里面提供了三角函数的计算。需要注意的是，必须先把角度转换成弧度才能带入计算。弧度的精度对于最终结果有一定影响，但是没有多大影响，可直接忽略。最主要的影响还是角度。

        当r足够大的时候，的角度变化量如果是1度，那么其坐标增量将会大于1，具体表现为离散不连续的坐标。如下：

        本次计算的圆的半径为1500，角度变化量为1度。可以看出，算出来的坐标，无论是x还是z轴，都是不连续的。这里以第一象限内点的坐标为例。如果要使坐标连贯，那么相邻的两个点的x和z的增量要大于等于0，小于等于1.

即且.（这里的x为角度变化量，也就是每次迭代的角度）。由于程序是从0度开始迭代，那么出现以下式子：

        只需要解出上述不等式组即可算出角度变化量的取值范围。（或许吧，反正我自己还没有试过） 。等我之后学到三角函数再把这个程序改进一下（挖坑.jpg）。我的同学用Lua语言也写了一个程序，并且加入了图形显示。但是目前他的程序还存在一定问题，所以暂不介绍。

        肯定会有更高级并且严谨的方法来计算圆上点的坐标，但是由于我知识水平有限，所以请嘴下留情。