法线变换的推算

之前一直不是很理解《unity shader入门精要》中的法线变化,网上查也不是很明白这里做一个所以自己就之前照着书中的公式做了一个推导过程。

Unity的空间转换都是对坐标/方向做3种和变换矩阵的矩阵乘法操作分别是位置偏移,旋转和缩小 。法线是一个方向所以位置偏移对它没有作用。

接下来我会二维坐标系中演示一个坐标为(0,0),(0,1),(1,0)的三角形并且在(0.5,0.5)上面画法线来测试旋转和缩小是否会对法线进行影响

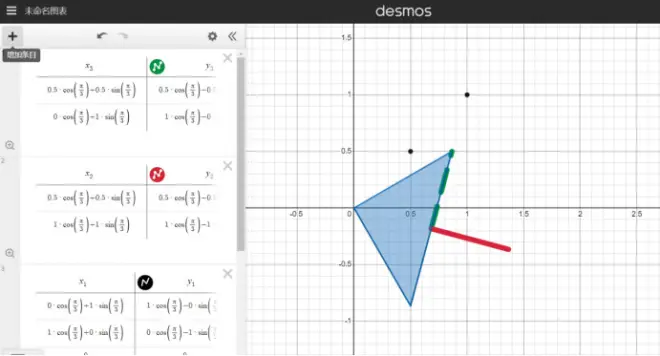
参考《Unity Shader入门精要》的方法,先假设一个变换矩阵(G)来变化空间A的法线(NA)到b空间,而空间B的切线(TB)等于用于空间变换的矩阵(MA->B)乘以TA(空间A的切线),由于法线和切线不同空间下都垂直得出公式可得:

进一步推导后可得

接下来我们来逐步分析这些公式:

第一步:

点积操作能变成转置矩阵相乘是因为一个1*n的矩阵乘以n*1的矩阵的矩阵和点积的计算方法都是相同的

第二步

这里依赖转置矩阵的性质

第三步

依赖矩阵的性质满足结合律不满足交换律

最后

TA的倒置矩阵乘以NA等于TA和NA的点积(和第一步性质相同)等于0.

而只有单位矩阵不影响这个公式

因此