前置内容

1)设输入信号函数为f(t)，系统的冲激响应为g(t)，则系统输出y(t)为f(t)与g(t)卷积。即：

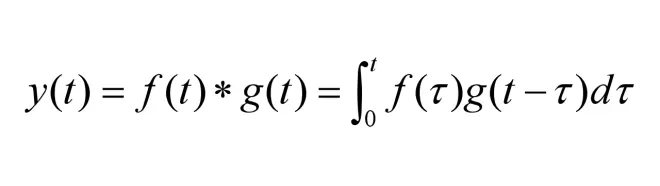
        因为卷积过程过于痛苦，所以一般使用拉普拉斯变换计算，即：

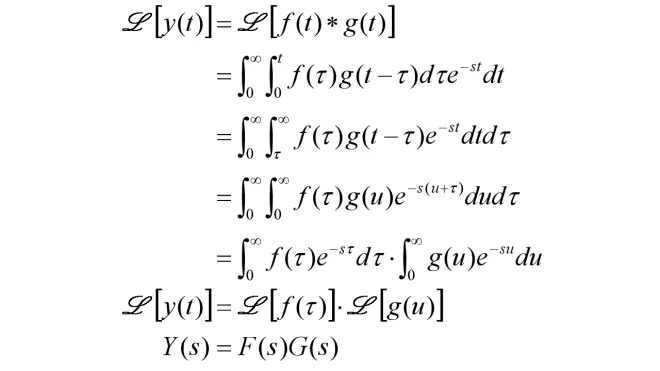
        可以看到输入信号f(t)与系统冲激响应g(t)的卷积，等于输入信号的拉普拉斯变换F(s)与系统的传递函数G(s)的乘积。即化卷积为乘积，简化了运算过程。

2)两个系统G和H串联时，输出y(t)为输入f(t)经过两个系统的卷积，根据(1)可得输出的拉普拉斯变换Y(s)为输入F(s)与两个系统的传递函数G(s)和H(s)的乘积，所以系统串联传递函数为G(s)H(s)，即：

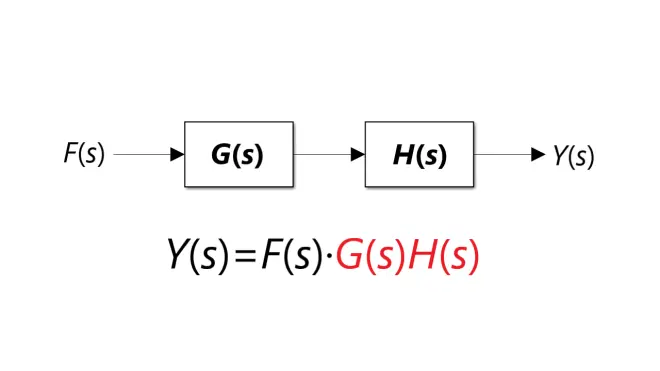
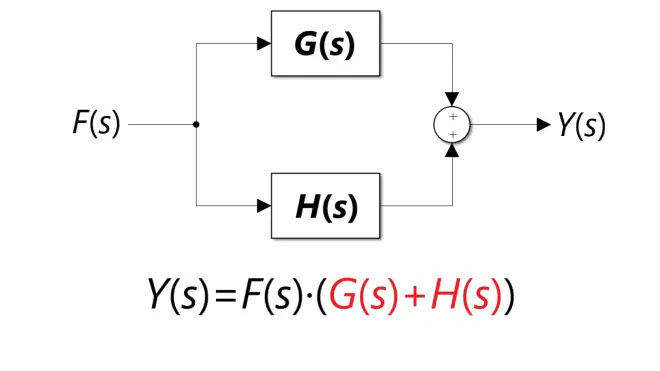
3)因为线性时不变系统满足叠加定理，所以两个系统G和H并联时，输出y(t)为两个系统的输出和，复频域上同理，输出Y(s)为两个系统的传递函数G(s)和H(s)的和，所以系统并联传递函数为G(s)+H(s)，即：

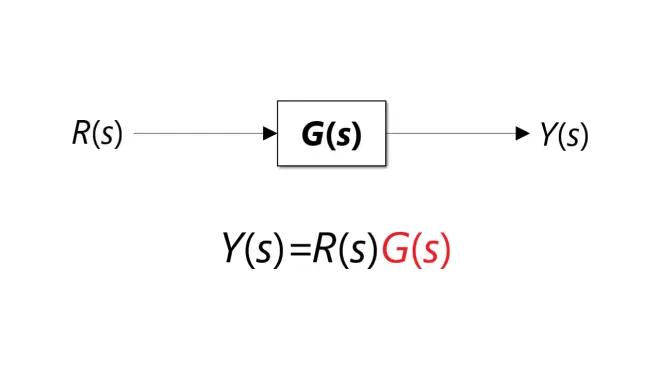
开环系统的传递函数(Open Loop Transfer Function)

        开环系统的输出与输入有关，但输入与输出无关，因为没有反馈。设输入为R(s)，系统传递函数为G(s)，则输出Y(s)=R(s)G(s)。

闭环系统的传递函数(Close Loop Transfer Function)

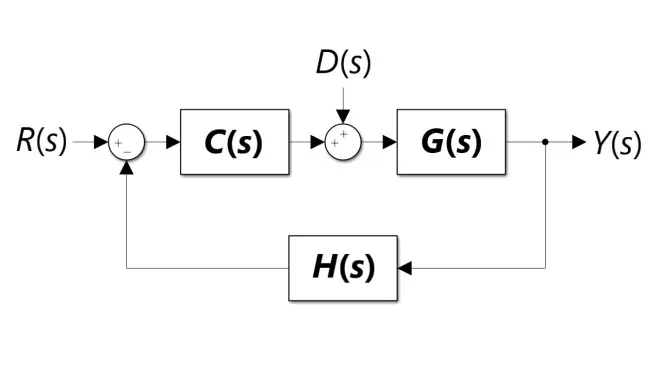
        当输出回馈到输入时，系统成为了闭环系统。如图6所示：

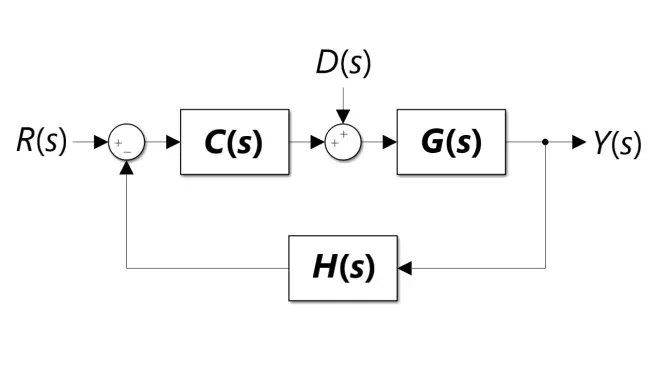
        其中G(s)一般为系统本征传递函数（被控对象），H(s)为反馈系统传递函数（一般为传感器），C(s)为控制系统传递函数（控制器Controller）。R(s)为控制参考输入（Reference），D(s)为外界干扰输入（Disturbance）。Y(s)为输出。现求其传递函数：

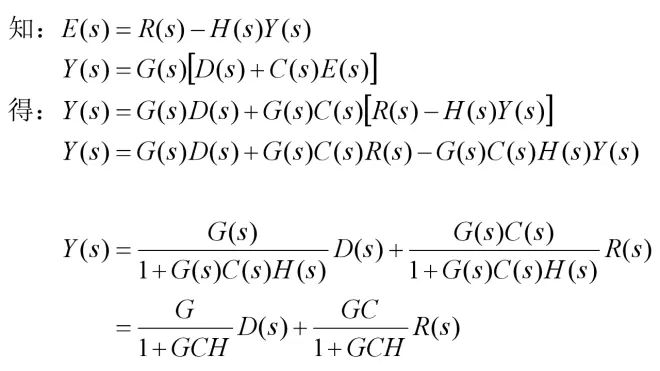
PS：E(s)为误差（Error），为参考减去反馈的差值。

        可以发现不同输入的闭环系统传递函数是不一样的。对于控制参考输入R(s)，其传递函数为GC/(1+GCH)；对于外界干扰输入D(s)，其传递函数为G/(1+GCH)。其输出响应框图用下图表示为：

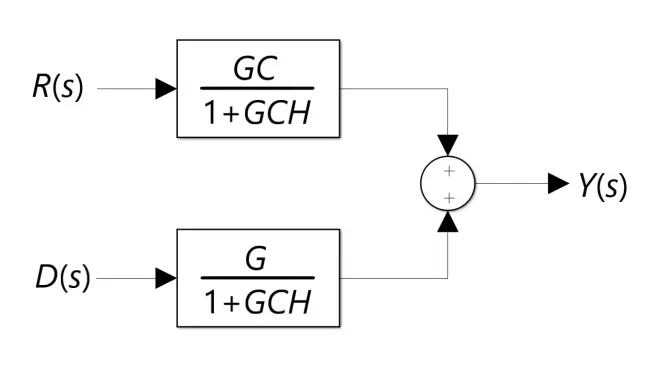
        在忽略干扰输入D(s)的情况下，一些教材会系统G和系统C会合并成一个系统G，此时传递函数简化为G/(1+GH)；一些教材会把H默认为1，而把C写作H，于是其传递函数变为GH/(1+GH)。

        系统控制目标为，让输出Y(s)达到并跟踪输入R(s)，且不受干扰D(s)的影响。系统G为被控对象，其函数往往与现实物理过程相关，而系统H和C是人为设计的。通过设计H和C来控制G使得完成控制目标。

        除了关注输出Y(s)，其误差E(s)（Error）也是值得关注的，它为参考值减去反馈的值，也就是控制系统C的输入，其表达式为：

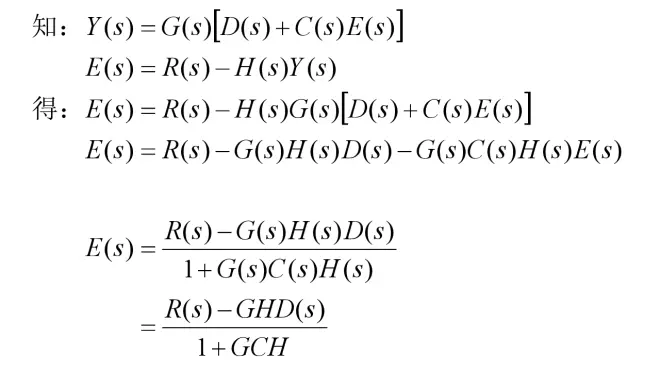
        一般情况下我们希望输出Y(s)达到并跟踪R(s)，也就意味着误差E(s)=0。令E(s)=0有两种手段：

       I：令分子等于零，即R(s)-GHD(s)=0；

       II：令分母等于无穷大，即1+GCH=∞。

       手段I有个问题在于，R(s)和D(s)一般是不可控的。因为R(s)和D(s)为系统的输入，不属于系统控制范围，除非R(s)=D(s)=0这种特殊情况，一般情况下分子是无法等于0的。而手段II中G、C、H都属于系统函数，特别是系统C、H都是人为设计的。所以可以使得1+GCH的值非常大以消除误差。

闭环系统的开环（环路）传递函数(Loop Transfer Function)

        观察前文可以发现，不管是R(s)输入还是D(s)输入的闭环传递函数，亦或者误差E(s)的表达式，其分母均为1+GCH。这个式子极为重要，因为方程1+GCH=0为闭环系统的特征方程，它的根为闭环系统的极点，所以它代表着整个闭环系统的响应特性。但由于特征方程极难求解（在没有计算机的年代），所以工程师们一般关注的是开环传递函数（或者叫环路传递函数），即GCH。实际上，当把闭环系统的反馈通路切断时，其反馈输出就是GCH，如图10所示：

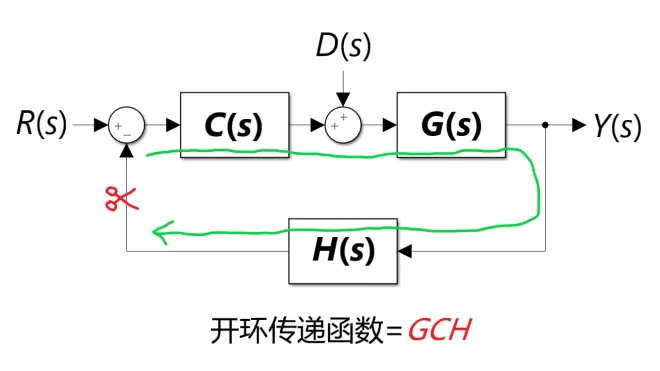
PS1：这里以输入R(s)为例。若以输入D(s)为例，其切断位置为系统C的输出端（加法器前），开环传递函数不变。

PS2：从图可以知道，其开环输出是指输入绕着环跑了一圈回到起点的输出，重点在“环”，其英文为“Loop”；而“开”表示的是切断回路，但英文的“Open”并无此意；“Open Loop”代表的是纯无反馈的开环系统。所以开环系统=Open Loop=G；闭环系统=Close Loop=GC/(1+GCH)；闭环系统的开环=Loop=GCH。

        在闭环系统中，开环传递函数没有具体的物理意义，因为实际操作中也不会切断反馈回路。但是开环传递函数比闭环传递函数好算，并且可以通过开环传递函数的性质推测出闭环传递函数的一些性质。在没有计算机的年代，就有科学家建立起这个沟通桥梁，如伊文思(w.R.Evans)的根轨迹法，奈奎斯特(Nyquist)稳定判据。

闭环系统稳态输出估算

        前文已经知道闭环系统的输出Y(s)=GC/(1+GCH)*R(s)+G/(1+GCH)*D(s)，现在对其表达式进行以下处理：

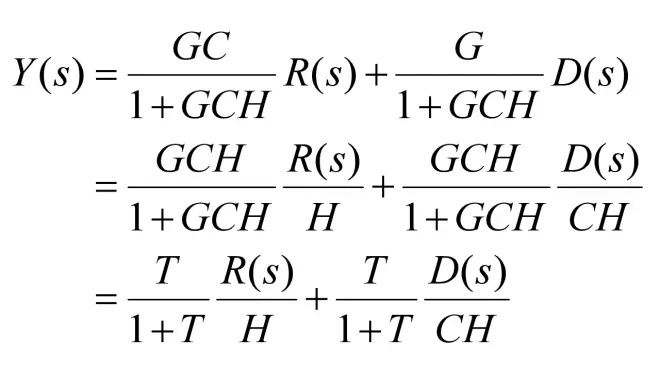
        此处用T代表开环传递函数T=GCH。同理，对于误差E(s)，也可将其表达式转为另一种形式：

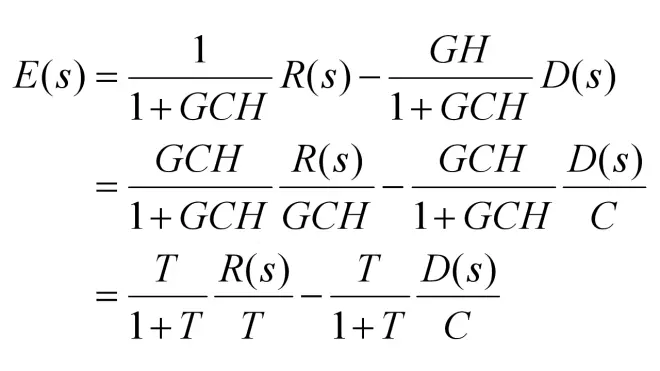
        当满足以下条件时，可以估算系统的输出Y(s)：

        I、闭环系统稳定，所有闭环极点均位于s平面的左半平面；

        II、输入R(s)、D(s)为有界正/余弦波时；

        III、系统已经过足够长时间达到稳态。

        因为任何周期信号均可以用傅里叶变换拆解成无数个正/余弦波叠加（包括直流常数，为频率=0的余弦波cos(0t)），所以此分析基本涵盖了系统的稳态响应。

        绘制开环传递函数T的幅值伯德图(Magnitude Bode Plot)，一般情况下，可以发现在低频区|T|的值非常大，而高频区|T|的值非常小。随着频率从低频区到高频区逐渐增大，|T|的值逐渐减小，最终穿过0dB轴（|T|=1），其对应的频率为截止频率。于是可以粗略地估算低于截止频率和高于截止频率的输出Y(s)。

PS：|T|也叫做开环增益/开环放大倍数/Loop Gain。

        低于截止频率时|T|的值很大，当|T|>20dB（>10）时，式T/(1+T)可以近似等于1；高于截止频率时|T|的值很小，当|T|<-20dB（<0.1）时，式T/(1+T)可以近似等于T。于是可以得出闭环系统的近似稳态输出Y(s)而近似稳态误差E(s)，如图13、14所示：

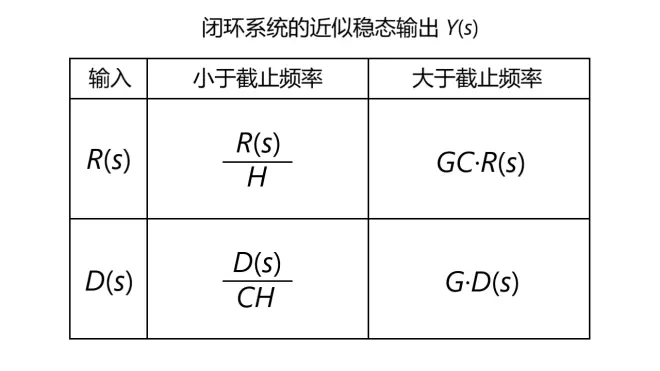
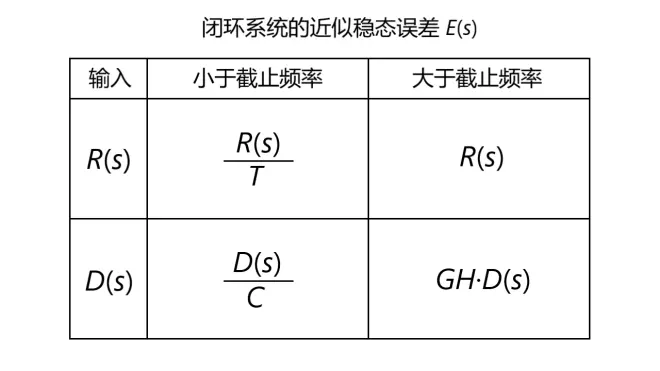
        通过上图可以得出以下结论：

        I、当输入R(s)的频率小于截止频率时，输出Y(s)仅与系统H（一般为传感器）有关，若H=1，则可以认为Y(s)=R(s)。

        II、当输入R(s)的频率较低时，稳态误差E(s)为|T|的倒数。也就是说开环增益越大，误差越小。当开环增益足够大时，可以近似认为误差为零。例如我曾经做过一个输出36V的开关电源[1]，直流开环增益|T|达到了120dB（1000000），意味着误差为36/1000000V。实际测试中精度0.001V的仪器都测不到输出偏差。

        III、当输入R(s)的频率高于截止频率时，由于GC的值很小了，所以输出约等于零。误差就等于输入本身了。因此可以得出，闭环系统的输出基本能达到并跟踪截止频率以下的控制参考输入，但高于截止频率的控制参考输入则无响应。

        IV、对于低频的外界扰动输入D(s)（比如重力），其导致的误差E(s)与系统C有关。若想误差为零，则需要C的值非常大（一般由积分器实现）。当C非常大时，就可以认为扰动导致的输出Y(s)等于零了。

        V、对于高频的外界扰动输入D(s)（白噪声，自然界有的是），其输出Y(s)仅与被控系统本征函数G有关。一般来说系统G与自然界的物理过程相关，绝大多数自然物理过程对高频是不敏感的，所以可以认为高频下G的值非常小，全靠G来屏蔽扰动输入。

附：[1]--https://t.bilibili.com/499488800854365924

        所以在设计闭环系统时对不同的输入情况，采取如图15所示策略：

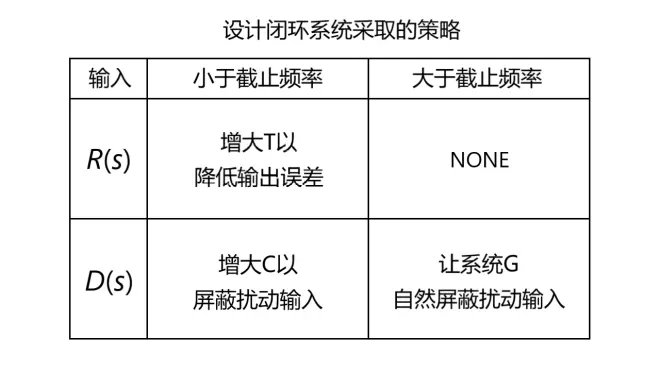
        注意，这里策略只是一个定性参考，一般是设计好后反向校验的，具体设计值按照具体问题具体分析。同时提醒G、C、H是函数，不是常数，我只是省略了后面的“(s)”。让C等于超级大的常数来屏蔽D(s)系统基本会出问题。在以后的专栏中我会给出详细设计过程（如果有的话），本文先当个基础的认识。（完）

 

by HD-nuke8800

2022/4/24