An Introduction to Modular Arithmetic

The best way to introduce modular arithmetic is to think of the face of a clock.

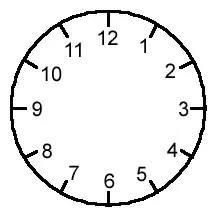
So 

13 becomes 1, 

14 becomes 2, 

and so on.

This can keep going, so when you get to "25 o'clock'', you are actually back round to where 1 o'clock is on the clock face (and also where 13 o'clock was too).

What we are saying is 

"13=1+ some multiple of 12", and 

"38=2+ some multiple of 12", 

or, alternatively, "the remainder when you divide 13 by 12 is 1" and "the remainder when you divide 38 by 12 is 2''. The way we write this mathematically is 

13≡1 mod 12, 

38≡2 mod 12

and so on. This is read as 

"13 is congruent to 1 mod (or modulo) 12" and 

"38 is congruent to 2 mod 12".

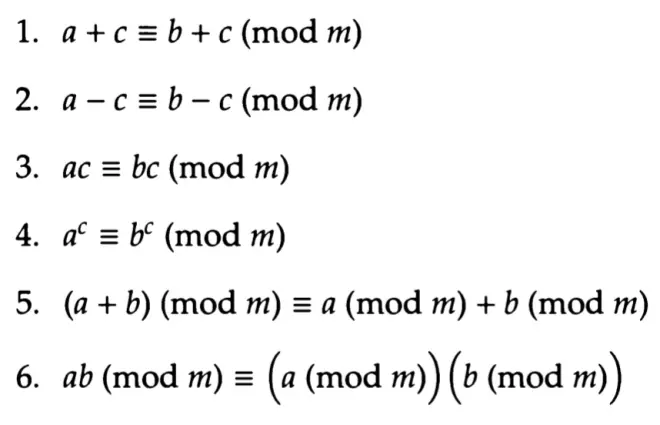
key words:

mod‧u‧lar /ˈmɒdjələ $ ˈmɑːdʒələr/ adjective 

con‧gru‧ent /ˈkɒŋɡruənt $ ˈkɑːŋ-/ adjective

congruence

re‧main‧der /rɪˈmeɪndə $ -ər/ ●○○ noun