数学实现信号分析[sin(jln(2+sqrt(3))-π/2)]: 补充

这里我们补充一下第二章我摸了的部分

第一章我说到了这个:

但是第二章我们得出了这个结果:

这个就真的很奇怪了, 这两条式子好像不存在任何关系, (编不下去了, 反正就是说一下这两条式子的关系)

第一条式子我们一开始就是假设f(t)是实函数, 那么算着算着复数就出来了

在第二章的计算过程中有一个这样的东西:

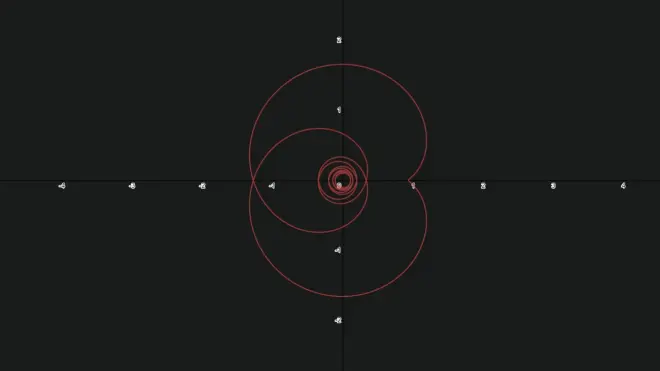
我们其实可以把里面的第n项画出来的(注: 这里用的是复平面, 所以实数轴对应的就是x轴)

这里可以看到虽然过程是复数, 但是加起来之后刚刚好就是实数了, 所以我们的结果是没有错的

第三条式子通过整理得到了第二条式子, 只是整理, 每一项都没有做变换, 那么当t=0时, 上图的红色和紫色就分别是cn和c-n了

我们记    |a+bj| = sqrt(a^2+b^2), 即上图线段的长度       arg(a+bj)为上图线段与实数轴的夹角

那么观察容易得出:    An=2*|cn|,    φn=|arg(cn)|

也就是说我们可以通过复数求得An和极其复杂的φn (回归第一章wwwww)

当然在计算过程中没有人会用第一条式子的, 因为cos的合拼和化简极其困难, 而复数虽然理解起来有点困难, 但是计算缺非常简单

辅助理解:   https://www.youtube.com/watch?v=r6sGWTCMz2k   (404警告)

↑  b站的3b1b官方账号还没翻译, 等哪一天出了就去看看吧  [微分方程概论-第四章: 但是什么是傅里叶级数? 从热量流动到圆圈画图]

话说每一章字数越来越少了, 大家有发现吗, 而且说得越来越难懂, 不过放小, 下一章开始就简单了