【数学竞赛-几何】四边形的余弦定理
2022-04-30 13:06 作者:Rotas-math_lover | 我要投稿
一.什么是四边形的余弦定理
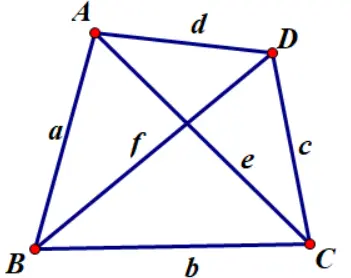
如图,记四边形的边
,记对角线
,则有
(这两个式子等价)

二.四边形余弦定理的证明
这个等式的形式看起来很像余弦定理,但我们只要稍微变下形,它就更像了,如下
这告诉我们,要构造一个角度为的 角,并且其两边分别为
,这样就可以用余弦定理直接证得
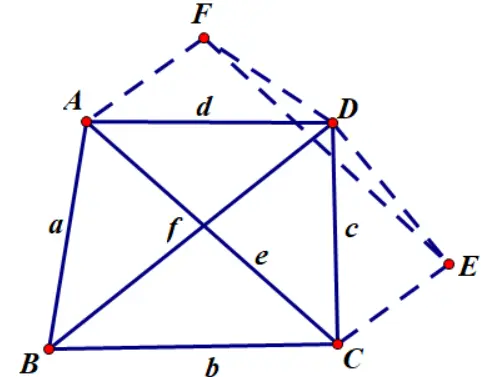
因此,我们以为边向外作
使得
因此,在中用余弦定理可得
从而,只要证到,这只需要证四边形
为平行四边形
观察图形,计算可得,因此,只需要证
这只需要证,根据相似,这个等式显然
故得证

三.四边形余弦定理的推广
若,则四边形
共圆,

此时四边形的余弦定理就变成了托勒密定理,如下

