最近我发现一位UP（B站：https://space.bilibili.com/328038328）竟然在做10x10完全下吸，时序采用我的套路，疯狂重走，而且做的还挺好。

"(º Д º*)

        回想起之前我搞完全下吸10x10的时候，自己想到了这套路，成功减少大量布线，体积比完全下吸9x9还小2333。不过显而易见的缺点是，由于反复重走，活塞有许多冗余的动作，最后导致门的运行时间非常长。
        那么完全下吸门的开门时间得多长呢？我分析了下我的套路，竟然还找到规律，那我不妨去算算开门时间。

        这里附上我曾经在2017年7月25号发布的10x10完全下吸门。各位可以仔细观察活塞运行动作，尝试寻找下规律。
        我分别统计了下吸1到下吸10电路运行所需要的时间，分别是4s，5s，14s，26s，58s，120s，250s，434s，813s，1638s。不过作图更容易找出规律。我作了个柱形图以及饼图。

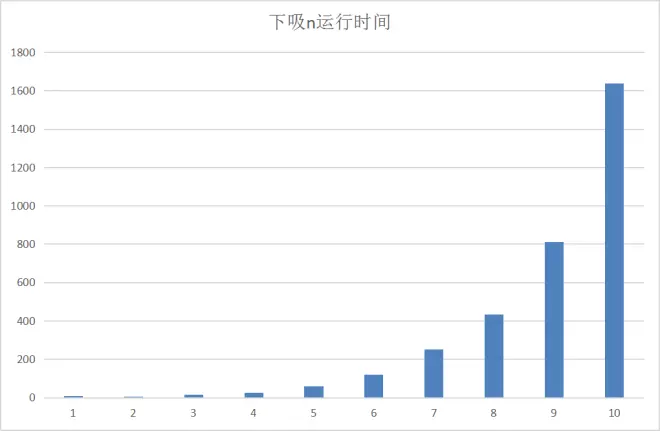
        很直观的感受是，下吸每增加一级，所用时间约是原来一级的两倍，即翻番。当然这只是初步判断，误差可能很大。不过，既然我已经知道时序的工作规律，为啥不建立一个数学模型去分析呢？

模型一

        不知道大家看我的视频是否发现这个规律，比如我要下吸第n层的方块，就要先把活塞运到第（n-2）层，然后运送观察者去激活活塞，方块被拉到第（n-1）层，接着把（n-2）层的活塞收回，最后把（n-1）层的方块收回。整个过程可以由下图表示：

转化成时序的话，如果要吸走第n层方块，则：

1、运行下吸（n-2）
2、推观察者上去，去激活，并收回观察者。
3、运行下吸（n-2）
4、运行下吸（n-1）
        可以发现除了第2步，别的都是重走（实际上第2步里也有重走成分），为了简化模型，我就当做第2步都是自己重新布线。按照这套路，经过简单粗暴的分析，即得到如下结果：

先说明下图中符号的含义：
        每一级下吸都有布线的成分（即非重走部分），这部分的运行时间记为tn，n为下标。而整个下吸n运行的总时间用Tn表示。重走时间要花费对应为Tn（除非中断重走），然后消去Tn，得到只含有tn的式子。现在，我得到了Tn需要重走多少个tn了，嗯哼？我貌似得到一个，数列？！

        是的，我得到一个数列，它是1，1，3，5，11，21，43，85，171，341，...
被老师骂考前还搞这么难的题后，我得到了这个数列的通项公式：

于是Tn和总开门时间Sn也有表达式了。

        那么tn是多少呢？这个就得实测了QAQ，既然我已经有个10x10活塞门了，那就拿它作样本咯。经过计算，可以得到tn的数据，t1到t7的数据分别为：4s，1s，1s，2s，4s，10s，14s。额，为什么没有t8，t9，t10的数据？
        因为在下吸8，我改变了时序，以便减少运行时间，所以已经不符合这个数学模型了。如果硬要代进去算，算得t8是一个负数。
(=′ー`) 
还是作图，观察规律。

用回归方程去拟合这些点

        这里我建立了两个回归模型，一个是指数模型，一个是多项式模型。可见多项式模型的R²值比指数模型的更大，即多项式模型的拟合效果更好。
这样我使用回归方程y=0.797619x²-4.55952x+7.42857来近似代表tn。合理外延，可以预测其它tn的大致数值。
        现在我就可以把数据放入电脑进行运算，得到下吸门单独下吸n的运行时间和总运行时间了。蓝色点代表单个下吸耗时，橙色叉叉是下吸到这一级的总时间，即开门时间，单位为秒（s）。

╮(￣▽￣)╭

嗯哼，晕了？不妨休息下，看一看如果要做到下吸20，50，甚至是100，运行时间大致多久？

        这里的单位是秒，也就是说，单纯下吸20所需时间是2163576秒左右，总开门时间是4326352秒左右，换算下大概是50天。

那么下吸50呢？

下吸50的开门总时间大概是147 3427个世纪。别怕，还有下吸100呢！

        换算下总开门时间大概是1.659x10^15 亿年。而宇宙大爆炸到现在都没有那么久，可见按照我这套路是不可能做到完全下吸100的。就算做出来，你也得需要加速10^28倍左右，目前来说，没有电脑能接受这个指令：“/tickrate 200000000000000000000000000000”

        这么比较的话，那些大型飞行器门简直就是高速门了，那些飞行器门工作的几个小时与这几十次方年比起来，不知快了多少倍。

_(:з」∠)_

模型二

        除了上面的工作模型，我看那位UP用的是不同的工作方式，那我不妨再建立一个模型分析下。

        观察他的视频，可以发现他是先把活塞和观察者一起推上去，这样可以省下不少时间（可能也和BE版不能瞬推方块有关），再一排排收回。那么：

我又得到了一个讨厌的数列，它是：1，1，2，3，6，11，20，37，68，125，230，...

算了四天之后，我得到这个数列的通项公式：

（╯' - ')╯︵ ┻━┻ 

于是可以写出单个下吸所需时间Tn和开门总时间Sn。

        我还是需要测出tn的值，既然那位UP主已经发布视频了，我就直接从视频里获取数据（虽然不太准），得到T1至T7分别为：7s，12s，25s，54s，102s，189s，354s，由此算得t1至t7分别为：7s，5s，6s，17s，16s，14s，26s。为啥没有t8以后的数据？因为视频里只到下吸7。绘制tn的散点图，这……

这些点怎么这么奇怪=_=，但还是用回归方程拟合一下：

毕竟点比较诡异，不知道用哪个回归模型拟合较好，于是我把三个不同的回归模型写出来：

I、3.0357x+0.8571。R²=0.7501

II、0.369x²+0.0833x+5.2857。R²=0.7834

III、4.098e^(0.2492x)。R²=0.749

      于是我根据三个不同的模型分别计算单个下吸的开门时间，并且与原数据进行比对，算出其残差和残差的方差：

        可以发现，使用II（多项式）模型的回归方程算出结果与实际值更加接近，其残差的方差也最小，并且R²值是三个模型中最大的。于是tn可以使用II回归方程近似代替。

        额对了，an的通项公式由于存在虚数，用于计算的程式并不能计算复数（也可能有这功能但我不会用），我在算通项公式时无意间推出了它的近似表达式，误差在0.1以下（n≥5），随着n增大，误差越小。

        现在可以把这些数据交给电脑，我预测下下吸8，下吸9，下吸10所需的运行时间。顺便也皮一下把下吸20，下吸50，下吸100也算下。图中蓝色点为Tn，单个下吸运行时间，橙色叉叉为Sn，为整个开门时间，单位为秒。

_(¦3」∠)_

        由图中数据可大致得出T8=653s，约10.9分钟；T9=1209s，约20.2分钟；T10=2234s，约37.2min。总开门时间Sn大约是S8=1467s，约24.5分钟；S9=2676s，约44.6分钟；S10=4910s，约81.8分钟（1h22min）。

继续皮，看一下下吸20，下吸50，下吸100所需时间。

        这里只看Sn数据，换算下时间S20大约是25.3天，S50大约6 0216.9个世纪，S100大约1.028x10^12 亿年。

 

        这时间确实是等不来的，不过对比上面的数据会发现一个蹊跷的地方。模型一是从PC java版的MC取数据的，而模型二是从基岩版的MC上取数据的，而且大家都知道java版的红石响应速度一般都快于基岩版，为什么模型一算出的结果比模型二的还大呢？一开始我也愣了一下，不过想了下这两个模型的区别就可以知道了。比较一下模型一的数列an和模型二的数列an，如果把an简化成等比数列来看，模型一的公比是2，而模型二的公比是1.839，虽然两者差不多，但是在n很大时，底数的微小差别也会被放大许多，这也是指数函数的特性。可见随着n增大，时序和红石的响应速度对时间的影响，前者影响更大。这也可以从我的10x10活塞门体现，从下吸8开始的时序已经和下吸7不同了，模型一计算出的开门时间是比实际偏大了700秒左右（反过来说就是我省下了700秒）。

        当然，tn我使用回归方程去代替，其本身的误差也比较大，而回归方程一般不宜外延，所以外延算出的数据这里仅用来参考，并不绝对，而且活塞门的制作过程各种延时是无法预测的，最终活塞门成品的运行时间与这些模型算出的时间存在几秒至几十秒的误差也可以接受。n越大，误差也越大，比如下吸50，误差几十个世纪都可以接受的，如果误差还是几秒，这模型也太准了吧。

        这篇专栏就到此结束惹，如果各位有更好的模型，或者发现我的计算上出现失误的话，欢迎在评论留言。

(￣▽￣)~*

在此感谢影叔（B站：https://space.bilibili.com/13658976/），瓜君（B站：https://space.bilibili.com/7486276/），无痕（B站：https://space.bilibili.com/66583959/）。