《几何原本》命题3.14【夸克欧氏几何】

命题3.14：

在同一圆内，等弦的弦心距相等，弦心距相等的弦也相等

已知：圆ABDC，弦AB,CD，点E为圆心，EF⊥AB，EG⊥CD

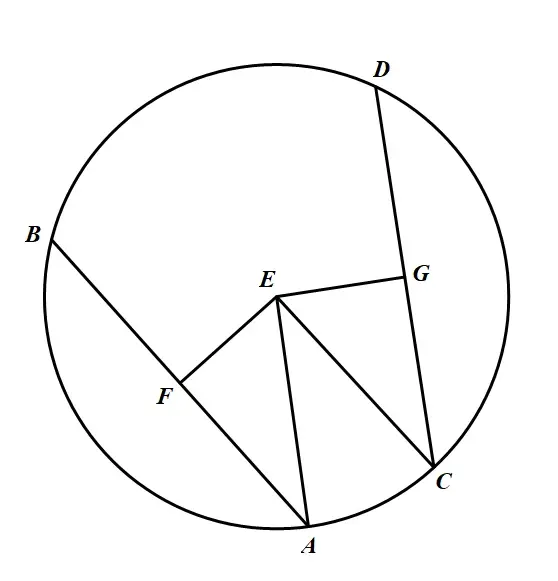
当AB=CD时

求证：EF=EG

解：

连接AE，CE

（公设1.1）

证：

∵点E为圆心，EF⊥AB

（已知）

∴AF=BF

（命题3.3）

∴2AF=AB

（公理1.2）

∵点E为圆心，EG⊥CD

（已知）

∴CG=DG

（命题3.3）

∴2CG=CD

（公理1.2）

∵AB=CD

（已知）

∴AF=CG

（公理1.1）

∵点E是圆ABDC的圆心

（已知）

∴AE=CE

（定义1.15）

∵EF⊥AB

（已知）

∴∟AFE是直角

（定义1.10）

∴Rt△AEF中，EF2=AE2+AF2

（命题1.47）

∴EF2=CE2+CG2

（公理1.1）

∵EG⊥CD

（已知）

∴∟CGE是直角

（定义1.10）

∴Rt△CEG中，EG2=CE2+CG2

（命题1.47）

∴EF2=EG2

（公理1.1）

∴EF=EG

当EF=EG时

求证：AB=CD

解：

同理可证，

AF=CG

Rt△AEF中，AF2=EF2-AE2，

Rt△CEG中，CG2=EG2-CE2

 证:

∵EF=EG

（已知）

∴AF2=CG2

（公理1.1）

∴AF=CG

∴2AF=2CG

（公理1.2）

∵2AF=AB，2CG=CD

（已证）

∴AB=CD

（公理1.1）

证毕

此命题将在下一命题中被使用