【种花家务·几何】1-2-07等腰三角形的判定『数理化自学丛书6677版』

2023-12-16 16:32 作者:山嵓 0人读过 | 我要投稿

【阅前提示】本篇出自『数理化自学丛书6677版』，此版丛书是“数理化自学丛书编委会”于1963-1966年陆续出版，并于1977年正式再版的基础自学教材，本系列丛书共包含17本，层次大致相当于如今的初高中水平，其最大特点就是可用于“自学”。当然由于本书是大半个世纪前的教材，很多概念已经与如今迥异，因此不建议零基础学生直接拿来自学。不过这套丛书却很适合像我这样已接受过基础教育但却很不扎实的学酥重新自修以查漏补缺。另外，黑字是教材原文，彩字是我写的注解。

【山话嵓语】我在原有“自学丛书”系列17册的基础上又添加了1册八五人教甲种本《微积分初步》，原因有二：一则，我是双鱼座，有一定程度的偶双症，但“自学丛书”系列中代数4册、几何5册实在令我刺挠，因此就需要加入一本代数，使两边能够对偶平衡；二则，我认为《微积分初步》这本书对“准大学生”很重要，以我的惨痛教训为例，大一高数第一堂课，我是直接蒙圈，学了个寂寞。另外大学物理的前置条件是必须有基础微积分知识，因此我所读院校的大学物理课是推迟开课；而比较生猛的大学则是直接开课，然后在绪论课中猛灌基础高数（例如田光善舒幼生老师的力学课）。我选择在“自学丛书”17本的基础上添加这本《微积分初步》，就是希望小伙伴升大学前可以看看，不至于像我当年那样被高数打了个措手不及。

第二章三角形——等腰三角形

§2-7等腰三角形的判定

【01】我们已经知道，一个等腰三角形的两个底角是相等的，如果有一个三角形，它有两个角相等，它是不是等腰三角形呢？这就很难说了指因为要判定一个三角形是等腰三角形，必须知道它有两条边相等。为此，我们来研究这一问题。

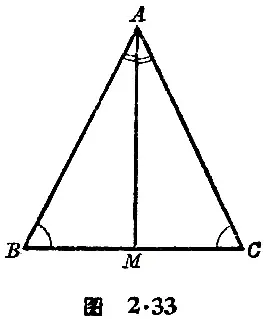
【02】画 △ABC，使 ∠B＝∠C（图2·33），画 BC 上的高 AM，因为 ∠AMB＝∠AMC＝d，∠B＝∠C，所以 ∠MAB＝∠MAC（等角的余角相等）。

【03】沿着 AM 把 △ABC 折迭起来，则 ∠MAB 与 ∠MAC 重合，∠AMB 与 ∠AMC 也重合，那么 AB 就落在 AC 上，MB 落在 MC 上，所以点 B 必然与点 C 重合（两直线只能相交于一点）。由此可知 AB 也与 AC 重合，所以 AB＝AC 。

【04】等腰三角形的判定定理：一个三角形如果有两个角相等，那末等角所对的边也相等，它就是等腰三角形。

例1.求证：等腰三角形中有一个角是 60°，它就是等边三角形。

【已知】△ABC 中 AB＝AC，∠A＝60°（图2·34）。

【求证】AB＝BC＝CA 。

【分析】要证明 △ABC 是等边三角形，只要证明 AB＝BC，要证明 AB＝BC，只要证明 ∠C＝∠A；也就是证明 ∠C 也等于 60° 。

【证】·

∵ ∠A＝60°（已知），

∴ ∠C＋∠B＝180°－60°＝120°（三角形内角和）。

又因 AB＝AC（已知），

∴ ∠C＝∠B（等腰三角形的底角相等），

就是 2∠C＝120°，

∴ ∠C＝60°，

由此可知，∠C＝∠A，

AB＝BC（等腰三角形的判定定理）。

∴ AB＝BC＝AC 。

就是 △ABC 是等边三角形。

【05】如果已知等腰三角形的底角是 60°，它的证明方法和上面的一样，也可得到同样的结论。希望读者自己来完成这个证明。

例2.求证：含有 30° 角的直角三角形中，30° 角所对的边等于斜边的一半。

【已知】直角三角形 ABC 中，∠A＝30°（图2·35）。

【求证】BC＝ $%5Cscriptsize%20%5Cfrac12$ AB 。

【分析】要证明 BC＝ $%5Cscriptsize%20%5Cfrac12$ AB，我们可以延长 BC 到 B 使 CB'＝BC，再证明 BB' 等于 AB 就可以了。

【证】∠BAC＝30°，我们已知 ∠ACB＝90°，延长 BC 至 B'，使 CB′＝BC，连结 AB' 。

可知 ∠ACB'＝∠ACB＝90°（邻补角），所以沿直线 AC 折迭，则点 B 落在点 B'，AB 与 AB' 重合。

∴ ∠B'＝∠B 。

又因 ∠B＝60°（30° 的余角）

∴ ∠B'＝∠B＝60°.

又 ∠BAB'＝2∠BAC＝30°×2＝60° 。

所以在 △ABB' 中，∠B'＝60°＝∠BAB'，

∴ BB'＝AB（等腰三角形的判定定理）。

但是 BC＝ $%5Cscriptsize%20%5Cfrac12$ BB'，

∴ BC＝ $%5Cscriptsize%20%5Cfrac12$ AB 。

也就是证明了 30° 角所对直角边等于斜边的一半。

【注意】本例还可以在 BA 上取 BM＝BC，再证明 MA＝BC，同样可证得结论。希望读者作为练习来证明。

例3.已知直角三角形 ABC 中，∠B＝60°，又 CD 是斜边 AB 上的高（图2·36）。求证 AC＝2CD 。

【分析】要证明 CA＝2CD，只要证得 CD 是直角三角形中对 30° 角的直角边就可以了。

【证】已知 △ABC 中，∠C＝90°，∠B＝60°，又 CD ⊥ AB，

所以 △ADC 也是直角三角形。

又 ∠A＝30°（直角三角形的锐角互余），

∴ CD＝ $%5Cscriptsize%20%5Cfrac12$ AC（例2的结论）

就是 AC＝2CD 。

例4.设在 △ABC 中，CF 平分 ∠BCA，过 A 作 FC 的平行线 AD 交 BC 的延长线于 D（图2·37）。求证 △ACD 是等腰三角形。

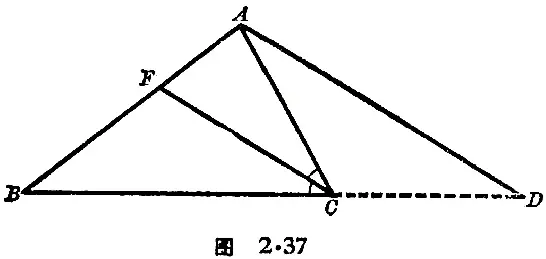
【分析】要证明 △ACD 是等腰三角形，只要证得 ∠CAD＝∠D 就可以了。

【证】

CF 平分 ∠BCA（已知），

∴ ∠BCF＝∠FCA 。

又 AD // FC，且 BCD 在一直线上（已知），

∴ ∠CAD＝∠FCA（平行线的内错角相等），

∠D＝∠BCF（平行线的同位角相等），

因此，∠CAD＝∠D（等于等量的量相等）。

∴ △ACD 是等腰三角形（等腰三角形判定定理）。

例5.一条船以每小时 15 公里的速度向北航行，上午 8 时到达 A 处，上午 10 时到达 B 处。从 A，B 望灯塔 C，并测得 ∠A＝42°，∠NBC＝84°（图2·38）。求从 B 到灯塔 C 的距离。

【解】

因为 ∠NBC 是 △ABC 的外角，

∴ ∠NBC＝∠C＋∠CAB，

就是 84°＝∠C＋42°，

计算得，∠C＝42°，

∴ ∠CAB＝∠C，

∴ BC＝AB（等腰三角形判定定理）。

又 AB＝15×(10－8)＝30，

即 BC＝30 。

答：从 B 到灯塔 C 的距离是 30 公里。

习题2-7

1、求证等腰三角形的两底角的平分线和底边构成一个等腰三角形。[提示：只要证得 ∠1＝∠2，就可决定 △BOC 是等腰三角形了]

2、在 △ABC 中，AB＝AC，又 PQ // BC，它与两腰分别相交于 E，F（如图）。求证 AE＝AF 。[提示：先证∠1＝∠2]

3、如图。如果我们要测量小河两岸 B，D 之间的距离。只要先测得 ∠ABD＝2∠ACD，再量 BC 的长，就可以得到 BD 的长，为什么？[提示：参考例5]

4、不用量角器，用直尺和圆规画出一个等于 60° 的角。[提示：从等边三角形的内角来思考]

5、要测量树的高度 AB，可以应用带有铅锤的等腰直角三角板 DEF，走到 K 处，使一直角边在铅锤线的位置（也就是与铅锤的那条线重合），沿着斜边 DE 看过去，正好看到树顶点 B（如下图）。.量得 AK 的长和测点与地面的距离（眼晴的高度）DK＝a 后，就得到树高 AB＝AK＋a，说明所根据的道理。[提示：其中 AK＝CD，只要说明 △BCD 是等腰三角形就可以了]