上节课（https://www.bilibili.com/read/cv8916897），我们阐述了复读机的具体作用机制，各种会减弱复读机实际表现的情况，以及如何合理选卡来尽量减少这些情况。这节课我们将继续学习如何对双分复读机的技能得分进行精算，以及基于该结果对不同N的复读单位进行强度排序。

        为什么选择双分复读机而不是常规复读机呢，是因为双分复读机里面没有概率up，每一轮前lvup发动次数是固定的，也没和分卡抢buff的存在。概率up可以抢lvup的buff，抢走后又可以影响lvup和其他卡的概率，而且概率up不是一直按固定N发动，也有近半会按照固定时间间隔连续发动。插入了概率up的常规复读队过于复杂，我感觉除了靠LLH用蒙特卡洛方法模拟，没有更好的方法了。

        好了，我们开始吧~

        上节课，为了探究复读卡组中不同卡的相互作用以及作用顺序，笔者做了一个复读N统计器，如下所示：

输入区：只需手动输入输入区的黄色格子，分别代表第一张Lvup、第二张Lvup、复读单位的N数，然后黄色下面的格子会按照倍数往下自动填充。

汇总区：会自动将输入区的结果汇总到一起，左边一栏是相应的N数，右边是什么技能触发了（1、2代表第1、2张Lvup，3代表复读）。输入区很长，到好几千N，不过汇总区只会汇总前999N，多余的不会进入汇总区。汇总区按N的先后排序，如果多个技能同N发动，则按321的倒序来排。

统计区：将汇总区的结果进行统计。通过数“3”的数量得到复读发动次数，两个“3”之间1和2的数量得到复读前lvup发动次数；并且同时统计得到2个lvup或任意lvup与复读之间同n或相隔1n的次数并统计。发动次数指满足条件的次数，并不一定真的发动。

        值得说明的是，如果两张Lvup同N发动，则仅记一次。如果Lvup和复读发生撞车，以Lvup垫底获得buff，即之前的buff还是给分卡，该Lvup的buff给下一轮来计算。例如112-168N这一段，记为：

        同N发动的多个技能按照3-1倒序排，1和2如果同N只记一次。因此112-140这轮Lvup发动了一次（1和2同N），140-168这段Lvup发动了三次。168N同时发生的Lvup则会延给下一轮计算。这个计算顺序与Lvup垫底获得buff的机制相同，利于复读机发挥，这也是为什么汇总时同N按照倒序排序。

        输入是自动表格做的，汇总和统计是vba做的，需要双击任意单元格后更新，我代码写的很乱就不放了（折腾了好几个二维数组倒来倒去）……

        至此，我们得到了复读队在一首999N的歌中，总共有几轮，每一轮前有几次Lvup，有几次撞车的具体数据。然而这些数据只是“满足了相应技能发动条件”，具体是否发动取决于技能的发动率。因此，下一节我们将继续计算各技能的发动率。    

二、Lvup实际概率与每轮实际被buff次数的期望值

        Lvup总共有20-24、26N共6张。同一个N的Lvup卡可能有不止一张，但它们的发动率和提升等级都是完全相同的。复读卡同理，整理得下表方便调用：

        一个复读队中，有两张不同Lvup，发动率也不同。如果一轮复读前Lvup发动2次，那很好算；如果发动3次，到底是aba还是bab，会影响具体概率，而之前写的统计器并没有统计那么细。所以为了计算方便，我们取两张lvup概率的几何均数，简化为对一张卡重复三次进行计算。如果发动1次或4次同理。

        由于Lvup叠两次到16级，2次以上没有意义，所以我们只统计0次数量、1次数量、2次及以上数量。可以excel直接调用二项分布函数，不过这比较简单，我们也可以直接算0次（(1-p)^n）和1次(p*(1-p)^(n-1)*n)后，再用1减就是2次及以上：

        然后，我们分别把复读前Lvup发动1-4次的次数，乘以后面的概率，再纵向相加，得到实际发动2次及以上、1次、0次的轮数的期望值。这一步全部由自动表格完成。

三、计算双分发动概率，制作最大加分卡表

将23-30N单次加分量最大的分卡信息汇总到下表方便调用：

分卡选择与下表一致。部分N出了单次加分量更大的分卡，不过我还是按下表来。

根据表中分卡概率计算双分卡全部发动、只发动1张、全不发动的概率：

四、具体得分计算

        我们把整个得分拆成两个完备事件组：一是lvup实际发动0次、1次、2级及以上；二是双分全部发动、发动1张、发动0张。然后对这3*3=9种情况计算后相加就得到了我们想要的得分。lvup实际发动次数的具体轮数的期望值我们已经得到，接下来就是算两者互相作用的时候的具体得分。

整理得：

        我们看该轮得分的最后一个格子。如果该轮Lvup没有发动，双分也没有发动，但复读机发动了。全队没有其他可以抢lvup的卡了，所以这是复读大概率复读到上一轮的分卡，我们需要加权上去：即

20.031/35*(0.4489*55860+0.4422*51745) +12.167/35*(0.4489*37018.5+0.4422*32903.5) +2.802/35*(0.4489*20369.25+0.4422*16254.25+0.1089*0) =39588。于是，我们得到了最后一个格子的值，填上去：

        我们上一次加权最后一个格子的时候，计算最后一项2.802/35*（……）时，把自己当成0计算的，现在这个格子有数据了，我们用新的数据再迭代一次：

        原则上我们还可以继续迭代，不过第二次迭代的增量已经很小了，再迭没啥意义了，所以我们到此为止。最后，把三块加起来，乘以2.5倍爆分宝石，就得到了双分复读的技能得分，整理得：

计算表格总览：

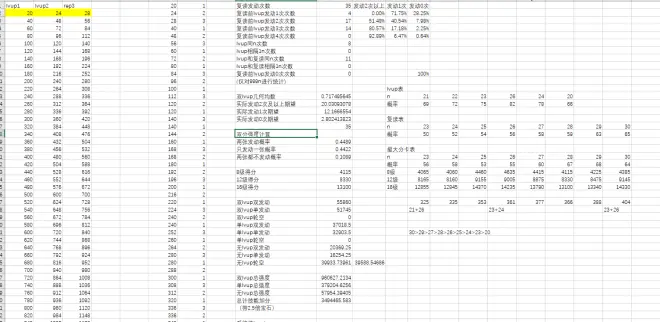
        上述计算过程都有自动公式，如果黄色输入区的N数更换后，具体概率数据都会直接根据右侧的表格直接调用，不用手打。只要输入黄色区后，双击任意单元格就可以直接得到最终数据。

        所以，20-24-28的复读机，999N曲目得分是349w。可见，其中单lvup、无lvup也占了不少强度。前人对复读机得分进行理论计算，往往局限于16级分卡的N数、最大加分量、概率，估算出的具体分值和实际情况相差甚远，均以失败告终。实际上，即使28-30N的长冲程复读机，也有近1/3轮数无法被buff到16级，只能buff到12级或仅8级；而23-26N的12级和8级的轮数占比会更高，虽然总轮数多，但平均每一轮的复读效率低。这在估算得分时是不能忽视的。

五、误差分析

这套计算方法不可避免的会有局限性：

1.       默认撞车后lvup垫底：实际情况是1:1，优先时非常影响得分，垫底则不影响。本计算仅取垫底。→有利有弊

2.       因程序设计所故，以两张lvup几何均数计算，而不是分开单独算。这在两张lvupN接近时问题不大，较远时可能会高估得分。（例如20和26N，20发动频率更高，在三次时20-26-20次数要比26-20-26更多，直接用几何均数估计会略微偏高）→高估→将在第六节中予以校正。

3.       两张lvup同帧发动仍然以几何均数计算发动率，而没算第二张额外增加的发动率。（例如两张同帧发动，几何均数为0.8，则该次实际发动概率仍然以0.8算，实际应该是0.96。虽然同时发动效果不叠加，但改帧发动概率是增加的）→低估。

4.       没考虑曲目中的双押。全部按无双押处理。→高估

5.       单双Lvup轮空当做本轮白费：实际上如果一轮中lvup发动后再轮空，会略微增加下一轮+16级的概率，这部分没有计算。→低估 →将在第六节中予以校正。

六、误差校正

        经核算 ，误差5非常影响最终得分，不能忽视。如果一轮中lvup发动后再轮空，会略微增加下一轮+16级的概率。低N复读机冲程短，复读效率低（指更多比例的轮数没法被buff到+8级，只能+4或根本不加），因为配套分卡发动概率大多不如高N的分卡，更容易产生轮空。误差5指本轮lvup叫了但轮空了，就会提高下一轮+4及+8的概率，但之前的计算予以无视。因此忽视这一部分之后，将严重低估低N复读机的得分。

        我们先对误差2进行校正，因为这比较容易：如果20N和26N的Lvup，一轮前满足发动条件2次仍然以几何均数计算，1次或3次采用加权几何均数计算。加权几何均数为20N发动概率的26次方，乘以26N概率的20次方，然后大家一起开46次方；其他N数同理。

        误差5的校正有点复杂，如下图所示。大致思路是算出Lvup发动2次，但轮空的轮数期望值，然后用Lvup ＞2/1/0 次的轮数/总轮数估算下一轮被Lvup各次的概率分别是多少。如果是2以上，则没有任何用处，无需校正；如果是1，则需要将相应轮数从Lvup1次扣除，加到2次上；0次同理。然后同样方法计算Lvup发动1次的后续。下表计算过程主要看红字和蓝字，灰字表示与校正无关，紫色是总结。

七、双分复读单位强度排序及理论计算实际表现验证

        我们基于该方法，固定某个N，通过反复尝试试出最佳Lvup组合，获得各个复读单位的最高分，并LLH实际模拟该组合，查看两者是否一致：

（虽然Lvup和复读同N不影响刷分，但我还是避免这种组合）

        由于我们需要对不同N数复读单位之间横向比较，曲目是999N，恰好被27整除，如果以此得分来比较其他不能整除的复读单位则会不公平。因此我们引入校正理论得分的概念，计算公式为实际理论得分/实际发动轮数（例如38）*带小数的发动轮数（例如38.42）。从上表来看，无论是否有+10%的概率加成，排行都是30>29>27>28=26=25>24>23>20。划等号的几者表现十分接近，没有本质差别。

        再看和LLH模拟的差值，会发现，本理论计算方法，比LLH模拟普遍高估。从误差分析来看，这部分高估可能来自撞车机制的不同，以及未考虑双押。我们假设这部分高估主要来自Lvup和复读单位的撞车机制处理不同导致，LLH为一半垫底一半优先，而本表格理论计算为全垫底。我们计算得出每一种组合的加权撞车数（直接撞车数+相隔1N的次数/4，因为双押大致占所有Note的1/4），将加权撞车数除以总轮数得到撞车影响的百分比（同样撞了5轮，23N的5轮和30N的5轮相差的分值截然不同，因此我们用撞的轮数除以总轮数来消除这一影响，变量设为b）；将表格与LLH相比高估的分值除以表格理论得分，得到差值百分比（变量设为a），两者行线性回归：

        可见，两者高度线性相关，R方=0.9，可以解释为，高估部分的90%均由于撞车机制处理不同而导致。将线性回归的拟合结果反过来校正表格的理论得分后，更换相应Lvup和复读单位后，只要别撞的太狠，得到的“拟合的LLH模拟得分”，与LLH的模拟得分几乎一致。因此使用本表格理论计算双分复读机得分结果可靠，且可用于Lvup的具体选卡参考。

八、一些发现&总结

        通过这些计算，有一些有趣的发现：本表格的理论计算和LLH并不完全一致。例如30N，本表得出的最佳Lvup组合是21+26，而LLH是23+26；实际上，因为23+26的加权撞车数更少，导致了LLH模拟更优，本表格仅考虑撞车垫底的情形，所以产生了不同；同理，由于30N质因数多，在搭配上不如质数的29或3的3次方的27，更容易撞车，LLH模拟的实际表现比表格差很多（约390-399w之间，表格是409w）；以及25N复读机LLH模拟略强于28N，也是因为25N的撞车比例更小，比28N更容易搭配。25,26,28三者差不多，26底卡难以获取；28由于上述原因导致实际表现可能不如25，这也可以解释为什么分榜上25N的多。

        单分的常规复读机由于插入了概率up，无法理论计算，只能通过直接LLH模拟获得。要排序的话，感觉就是堆工作量，lvup卡排列组合一下15种组合，概率up选32N善（不一定最强，但至少能位于中上，能有代表性），分卡是最高分固定的，曲子也固定一个（樱拜或妮可不理），属性手动设为1，观察指标设为1%或10%得分，模拟8*15次结果就出来了。

        不过我觉得双分不强，单分也强不到哪里去，两者应该是一致的，这个也可以为单分复读强度排序提供参考。

全文到此结束，欢迎评论，指正，探讨~