e^x泰勒展开的部分和多项式根的分布
的泰勒展开如下:
其部分和多项式为
一个显而易见的等式是:
利用上式,再结合数学归纳法容易证明,当n是奇数时,有且仅有一个实根,实根随n单调递减;当n是偶数时,
没有实根,有且仅有一个正的极小值点。2012华约自主招生考了结论。参见
https://wenku.baidu.com/view/20088d6359fb770bf78a6529647d27284b7337dc.html ,第14题。
下面两个视频也介绍了的一些性质。

下图就是 的全部复数根在复平面上的分布,
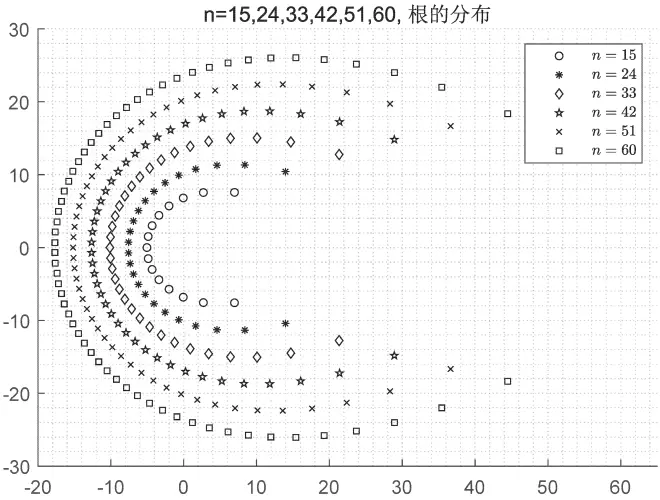
上图充分体现了Lucas定理:设是一个复系数多项式,则
的零点落在点
构成的凸包之内。对平面点集的凸包做一个通俗的解释:在每个点上插一颗图钉,然后用一根拉长的橡皮筋从外围去套这些图钉,橡皮筋收紧以后所形成的凸多边形就是这个点集的凸包(如下图)。
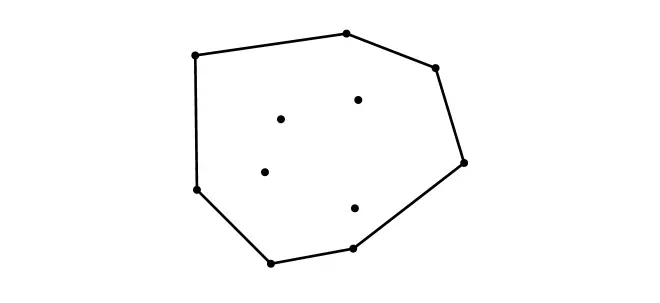

当时,
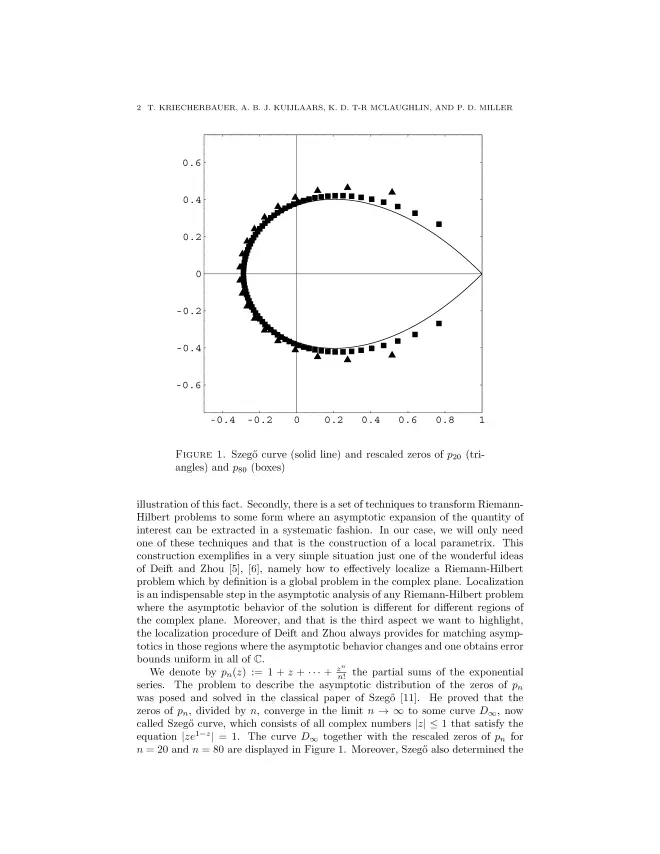
的全部复数根除以n后,渐近分布在
曲线上,写成复数形式为
,或者
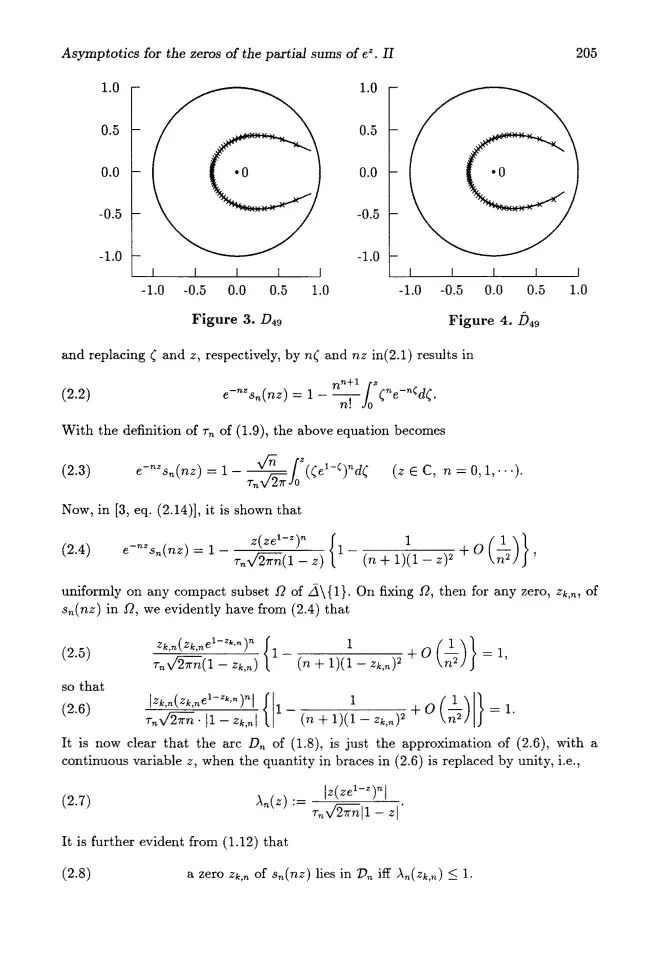
,这被称为Szego曲线,参考文献如下:
G. Szego, Uber eine Eigenschaft der Exponentialreihe, Sitzungsberichte der Berliner Math. Gesellschaft 21 (1922) 50–64.
R.S. Varga, A.J. Carpenter. Asymptotics for the zeros of the partial sums of $ e^z $.II. Computational Methods and Function Theory, 1990.
Kriecherbauer T, Kuijlaars A, Mclaughlin K, et al. Locating the zeros of partial sums of exp(z) with Riemann-Hilbert methods[J]. Mathematics, 2008, 458.
Dupuy T, Mclaughlin D T, SZEGO CURVES, STEEPEST DESCENT ANALYSIS AND THE ZERO BEHAVIOR OF PARTIAL SUMS OF THE EXPONENTIAL FUNCTION, 2005.
Buckholtz J D . A Characterization of the Exponential Series[J]. American Mathematical Monthly, 1966, 73(4):121-123.
Peter Walker. The Zeros of the Partial Sums of the Exponential Series.[J]. American Mathematical Monthly, 2003.