定音鼓研究

首先我们拿到一个定音鼓：

把其他乱七八糟的先扒掉，抽真空。剩下一个一个理想二维膜面，位于真空，没有弯曲刚度和剪切刚度。周边固定，发生小振动。写出其Lagrange量密度：

带入Euler-Lagrange方程得到经典的振动方程：

分离出时间振动部分，变成一个Laplace算子的特征值问题：

于是我们得到了正交的振动模态以及对应的振动频率（即特征值）。特征值的渐进行为由Weyl定理刻画：

虽然对于圆形鼓可以严格求解，但是Weyl定理告诉我们的已经足够多了：二维鼓的泛音列是按照\sqrt{n}规律增长的。何况总有一些奇怪的民族造出一些奇怪的东西来

现在我们带上空气玩（刚度的影响微不足道）。这样这个体系需要用三个PDE刻画，鼓内的空气，鼓面，以及鼓外的空气。鼓捣一番之后，我们消元拿到一个微分-积分方程

这相当于在原来的Laplace算子特征值问题里加上了一个微扰项。然后我们就可以做数值计算，算出相比于原来的泛音列的畸变。

拿出matlab仔细算一下：理想鼓的前四个泛音是1.00 : 1.34 : 1.66 : 1.98，带上空气之后变成1.00 : 1.51 : 1.99 : 2.46。物理能告诉我们的到此为止。这么一串泛音列传到我们耳朵里边好不好听，就是心理的范畴了。

一串乱七八糟的泛音列传到我们耳朵里，听起来有没有音高，音高有多高？所谓的missing fundamental效应声称感觉到的基频音高会偏向于泛音列的最大公约数。如果没有最大公约数（比如1和\sqrt{2}这种没有简单整数比的），就没有明显的音高感。这就能解释纯五度好听：如果是A4出发的纯五度，泛音列就是440,660,880,...能给出很好的音高感来。

这事情到底是怎么回事，首先我们可以想，简单整数比周期的正弦波叠加起来会不太乱，所以最大公约数的出现不是没道理的。

有的理论认为人对音高的感知基于自相关函数。假设我们有一个泛音列：

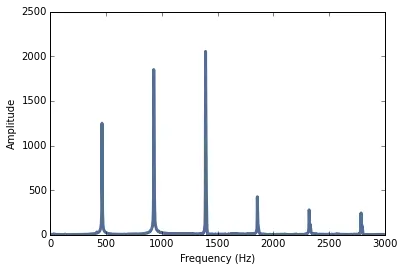
其自相关函数是

自相关函数的第一个峰值对应着感知到的音高464Hz。如果我们把基频去掉：

自相关函数的变化不大：

所以感知到的音高没变。看起来还是比较优雅的一个理论，但是是否符合听觉机制还有争议。

回到定音鼓。理想鼓的前四个泛音是1.00 : 1.34 : 1.66 : 1.98，没有简单整数比，所以没有音高感；带上空气之后变成1.00 : 1.51 : 1.99 : 2.46，接近于简单整数比，所以能够听到0.50的音高，所以才叫定音鼓。于是这乐器大约就是这样。