《超弦和M理论导论》第1部分第1章1.1

第1部分

半经典量子化和路径积分

————

第1章

路径积分和点粒子

1.1为什么选择弦？

    当今最大的科学刺头之一就是统一现代物理的两个基本理论——量子场论和广义相对论，并成一个理论框架的斗争。显然，两个理论组合体现出人类对最基本的自然力的全部知识的整个的总和。譬如量子场论业已在现象上成功解释小到10^-15厘米的微观物理规律。相反，广义相对论对完整和谐的统一体系的大量度行为的解释则无可匹敌，提供了一个迷人又信人的对宇宙本身起源的描述。这两个理论惊人的成就在于二者合并后可以解释大到40个数量级，从亚核子到宇观领域的事件和能量行为。

    然而，两个理论整体的不可相容性已经成为前五十年的巨大谜团。就好像大自然有两个脑瓜，每个脑瓜在它自己特殊的领域独立于另一个脑瓜工作，造成它俩整体的分离。为什么大自然要在它最底下最基础的层面上要求两个完全不着边的框架、有两套数学计算、两套假设以及两套物理原则呢？

    理想上，我们想要有一个统一理论来统一这两个基本理论：

然而，历史上过去几十年对这两个理论统一的尝试都很糟糕。他们不可避免地充斥了无穷或者

————

4

违背了一些物理学所持守的原则，比如因果律。过去几十年在量子场论中发展的重整化理论纵有高强的技术，也没能根除量子引力产生的无穷。显然，基本的一片拼图还不知道在哪里。

    尽管量子场论和广义相对论看上去完全不能相容，过去二十年间如火如荼的理论研究却已经把一件事搞得越来越清楚，那就是这个谜团的秘密最有可能潜藏在规范对称性（gauge symmetry）中：大自然最显著的特征之一是它的基本定律在用群论的方式表达时具有很大的统一性和对称性。通过规范对称性的统一显然是物理学的主课。特别是在杨-米尔斯（Yang-Mills）理论中用到的局部对称已经多次成功清除了量子场论产生的无穷，统一了带电粒子物理的法则为全面的框架。大自然看上去不只是因为美学而将对称性纳入物理定律。大自然需要（demands）对称。

    然而问题已经变成这样，即使是强大的杨-米尔斯规范对称性和爱因斯坦方程的广义协变也不足以得到一个有限的量子重力理论。

    现在对两个基本理论最有希望能真正统一和有限化描述的就是超弦理论和它的最后阐述M理论。至今超弦拥有已在物理上发现的最大号的规范对称性，也许大到甚至能消除所有量子引力的发散。超弦对称不仅包括爱因斯坦广义相对论和杨-米尔斯理论的对称性，也将超引力和大统一理论纳入它的子集中。

    粗略说说超弦理论解决谜团和无穷的方法，在图1.1很形象，这里我们通过求和一个带环的费曼图的无穷集计算两个点粒子的散射。这些图普遍上有相似之处，和“掐去”其中一条内线直到图像的拓扑结构改变相一致。

————

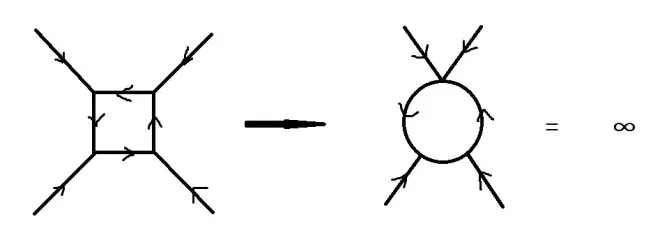
5

相比之下,在图1.2中我们画出了两个闭合弦状态散射的单环贡献。注意到我们不能像对待点粒子一样“掐掉”其中一条内线。因此，我们自然猜测超弦理论的发散更少甚至达到有限，因为对称禁止拓扑结构的改变。

    任何能够同时消除S矩阵的无穷以及将量子力学、广义相对论、大统一理论和超引力合并的理论显然具有令人窒息的美与复杂的数学运算。事实上，甚至数学家们也已经被超弦中出现的数学惊呆了，它将一些最不相像、领域跨度大的数学学科联系了起来，譬如卡茨-穆迪代数、黎曼（Riemann）表面和泰希米勒空间、模块化群，甚至是魔群理论。

    然而，弦理论很讽刺的一点是理论本身并不统一。（The great irony of string theory,however,is that the theory itself is not unified.）对于第一次学习该理论的人来说，它通常是一个令人困惑的混乱的民间传说、随机经验法则以及直觉。这个模型的很多公理曾一度似乎没有任何规律和理由。对于一个声称给出所有物理定律的统一框架的理论，结果这个理论本身都不是统一的，这也太讽刺了！该模型的秘密在最基础的层面上还有待发掘。

    通常当我们提出一个量子理论时，我们会从理论的几何学或对称性出发然后给出作用量。相应地从作用量中我们推出该模型的所有推论，包括单S矩阵。因此，一个正则量子化的（second quantized）作用量是阐述一个量子场论的合适路线。超弦理论似乎一度成为一个显然是随机传统的松散组合，基本原因在于它常常是用半经典量子化来阐述的。因此，我们必须拿来直觉和民间传说，来为一个统一理论构建所有费曼图。我们希望M理论（或者可能是更高级的理论）能够统一超弦理论到一个简洁有条理的形式上来。M理论已经能统一五种不同的超弦理论到单一理论中。最后可能只有一个单独的方程（也许写下来甚至没有一英寸长）来统一整个理论。

————

6

    不幸的是，超弦的几何学和膜是该模型有待发展的最后特征之二。实际上，从这个角度上来看，这个模型已经在过去30年逆向（backward）发展——从1968年它的量子理论的偶然发现开始！

    相比之下，当爱因斯坦第一次发现广义相对论时，他是从物理原则出发，比如等价原则，再用广义协变的语言阐述它了。一旦相关几何学建立，他之后就给出作用量作为问题的特解。之后，以曲流形的方式发现经典的方程解决方案了，提供宇宙的大量度行为下首个成功的理论模型了。最后，广义相对论发展的最后一步是引力量子理论的发展。因此这广义相对论历史性的发展的关键步骤可以表示为

        几何学→作用量→经典理论→量子理论。

    此外，广义相对论和杨-米尔斯理论是成熟的理论：它们都可以从第一原则阐述，这凸显理论背后的几何学和物理学假设。超弦理论和M理论才刚开始进入发展的舞台。

    显著的是杨-米尔斯理论和引力理论是两个简单几何学状态的特（unique）解：

（1）整体对称

        自由理论必须传播纯粹的无鬼自旋1和自旋2场变换作为SU()和洛伦兹（Lorentz）群的不可约表示。

（2）局部对称

        理论必须在局部上满足SU()和广义协变。

    显然的是共轭杨-米尔斯引力作用量是这两个简单原则的特解

    （第一个原则包含理论真材实料的物理。它不能作为第二个原则的子集被涵盖进去。这里有一个广义协变的无穷大数和SU()对称不变性，所以我们需要把第一个原则加进物理中并选择基本场的不可约表示。通过“纯粹”场，我们是说至多含有二阶微分的无鬼场，排除R2和F4更高阶微分的理论）

    问题仍旧是：超弦理论和M理论在这两个简单原则对应的是什么？（What is the counterpart to these two simple principles for superstring theory and M-theory?）

    当然，这本书的计划，必须反映出该理论已经逆向演化的事实。由于教学原因，我们将更多地跟随该理论的历史发展。因此，这本书第1部分，介绍半经典量子化的部分，将在某些时候表现为没有任何引导原则的传统

————

7

松散组合。这就是为什么我们选择第1部分强调泛函路径积分（path integral or functional）上手弦理论。只有用费曼路径积分我们才能得到一个形式以搞出其他形式，比如谐振子形式。虽然半经典量子化的路径积分形式仍然很令人悲哀地不充分，但是相比一个完全正则量子化的理论，它是粘结半经典量子化松散之尾的最方便的形式。

    本书第2部分我们将讨论场理论自身，从中我们能从一个作用量推出该理论的所有推论。然而，我们已经再次按照历史顺序逆向介绍场理论。

    第3部分我们介绍弦的“现象学”。虽然从10^19千兆电子伏特为起点做现象学可能有点冒昧，但是建立该理论做出的种种预测是很重要的。

    最后第4部分我们介绍二象性和11维M理论，第一次让我们观测弦理论的非微扰领域，该理论在这里和像是p膜和D膜的东西共存。

    不过，为了真正感受超弦理论的成功和可能的缺陷，我们必须首先试着去理解困扰了物理学家五十年的历史遗留问题。让我们现在给规范理论的发展做一个短评以感受组建引力有限理论的困难。我们也将简单触及超弦理论的历史发展。