我在B站上大学!【完整版-麻省理工-微积分重点】全18讲！学数学不看的微积分课程

P1-4 The big picture of Calculus

Calculus is about the connection between Function 1 and Function 2

• Function 1: Height y = f(t)
• Function 2: Slope S = y' = df/dt - the derivative of y
• Function 3: Bending B = y'' = d²f/dt² (d second f d t squared) - the second derivative of y

If we know y' and y'', we can find the max/min of the function 1

Max & Min

S = y', which is the derivative of y

• when y' = 0 , y = Max/Min;
• y' < 0 , y is going down;
• y' > 0 , y is going up.

B = y'', which is the second derivative of y

• when y'' = 0 , y = inflection point;
• y'' > 0 , y is a convex curve(bending up) , if y' = 0 and y'' > 0 , y = min;
• y'' < 0 , y is a concave curve(bending down) , if y' = 0 and y'' < 0 , y = max.

Some Important Functions of Calculus:

• y = x^n dy/dx = n*x^(n-1)
• y = sinx dy/dx = cosx
• y = e^x dy/dx = e^x

P5 The Exponential Function

the first differential equation: dy/dx = y

• when y = e^x, its slope is equal to itself - y' = dy/dx = e^x = y
• when y = c(e^x), dy/dx = c(e^x)
• the differential equation means an equation involves the function and its slope.

Base on this equation, we can prove (e^x)*(e^X) = e^(x+X)

• first step:
• reconstruction the function e^x that starts at e^0 = 1
• because n! will grow much faster than x^n, finally the number of (x^n)/n! will get extremely small and then the sum of this series comes to a limit

• second step: times two functions

Based on the reconstruction function:

• the number e is the sum of the exponential series when x = 1, rounded to 2.71828...

The graph of the function y = e^x

Example: computing compound interest

the second differential equation: dy/dx = cy

• when y = e^cx, dy/dx = y' = c(e^cx) = cy

P6 Integrals - from df/dt to f(t)

function 2 → function 1 : f(t) = ∫s(t)dt

Integral = function 1 = the area under the graph of function 2

P7 Limits and Continuous Functions

different types of limits：

an → A as n → ∞

1. infinite limits (A = ∞)
2. some positive number (A)
3. zero（A = 0)
4. ......

some special limits:

1. an - bn → A - B = ∞ - ∞ (no answer, could be zero( an = bn = n), could be ∞( an = n^2 and bn = n), danger part in mathematics)
2. an * bn → A * B = (0)*(∞)
3. an/bn → A/B = 0/0 or ∞/∞
4. (an)^bn → A^B = 0^0 or 1^ ∞

(1+1/n)^n → e

(1+1/(n^2))^n → 1

(1+1/n)^(n^2) → ∞

L'Hôpital's rule(洛必达法则)

If f(x) → 0 as x → 0, g(x) → 0 as x → 0,

f(x)/g(x) → △f/△g = (△f/△x)/(△g/△x) → slope(f)/slope(g)

exception:

f(x) = √x , the slope of f(x) is infinite, and the L rule doesn't work

when f(x) = √x at x = 0, slope not defined, but f(x) is continuous

if a function's got a slope that function's got to be continuous（可导必然连续，连续不一定可导（这里中英文字幕有点对不上））

Continuous：

if |x-a| < δ, then, |f(x)-f(a)| < ε

（当 x 落在a ± δ，f(x) 一定落在 f(a) ± ε）

P8 Derivatives of Sine and Cosine

To show d(sinx)/dx = cosx; d(cosx)/dx = -sinx:

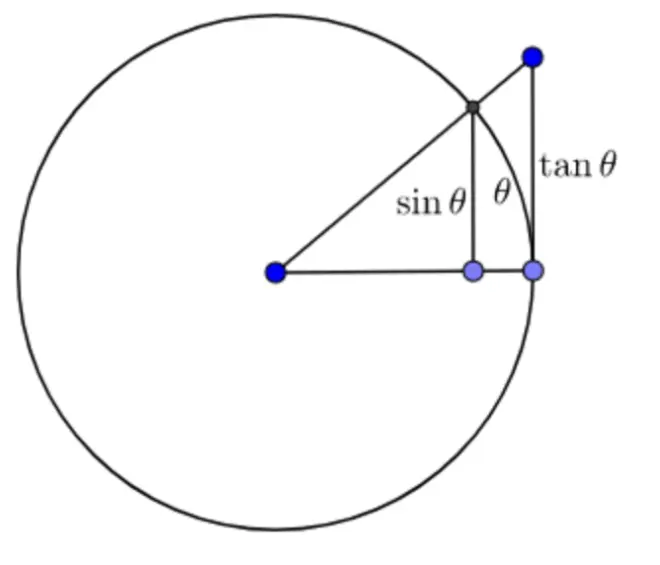
The first step: to show the limit of sinθ/θ → 1

sinθ < θ, θ > 0

∴ sinθ/θ < 1

tanθ > θ, 0 < θ < π/2

∴ tanθ = sinθ/cosθ > θ

∴ 1 > sinθ/θ > cosθ

prof. : maths always get some little trick

_ can't agree more!

∴ when θ → 0, sinθ/θ → 1

The second step: to show Δsinx/Δx → cosx, Δx → 0

sin(a+b) = sina*cosb + sinb*cosa

The third step: to show Δcosx/Δx → -sinx, Δx → 0

cos(a+b) = cosa*cosb - sina*sinb

Δcosx/Δx = (cos(x+Δx) - cosx)/Δx = (cosx*coxΔx - sinx*sinΔx-cosx)/Δx = cosx*(cosΔx - 1)/Δx - sinx*sinΔx/Δx

(cosΔx - 1)/Δx → 0

当x = 0, cosx = 1, y取得极大值，在该点的斜率是0，又可表示为 (cosΔx - 1)/(Δx - 0) = (cosΔx - 1)/Δx → 0

sinΔx/Δx → 1

∴ Δcosx/Δx → -sinx

P9 Product Rule and Quotient Rule

（一）Product Rule

ΔuΔv is negligible

∴ d(u*v) = uΔv + vΔu

∴ d(u*v)/dx = u*Δv/Δx + v*Δu/Δx = u*v' + v*u'

（二）Quotient Rule

P10 The Chain Rule

Discovery of chain rule

Δz/Δx = (Δz/Δy) * (Δy/Δx)

Example:

z' = -xe^(-(x^2)/2)

z'' = -x(-xe^(-(x^2)/2)) - e^(-(x^2)/2) = (x^2 - 1)e^(-(x^2)/2)

P11 Inverse functions and x = lny

y = f(x) and x = f⁻¹(x)

The function that have an inverse function have to be one-to-one: one x for one y, one y for one x

f(x) = y = e^x

f⁻¹(x) = x = lny - the natural logarithm

***x is the exponent, so the logarithm is the exponent in the original funciton

Key facts of logarithm

1- ln(y*Y) = lny + lnY

y = e^x and x = lny

Y = e^X and X = lnY

y*Y = (e^x)(e^X) = e^(x+X)

ln(y*Y) = lne^(x+X) = x + X = lny +lnY

2- ln(y^n) = n*lny

P12 Derivative of lny and sin⁻¹y

y = e^x and x = lny

To show d(lny)/dy = 1/y

ln(e^x) = x

(ln(e^x))' = 1

= (lny)' * e^x - chain rule

∴ (lny)' = 1/(e^x)

y = e^x

∴ (lny)' = 1/y

y = sinx and x = sin⁻¹y

y = sin(sin⁻¹y)

y' = 1 = cos(sin⁻¹y) * (d(sin⁻¹y)/dy)

x = θ

= cosθ * (d(sin⁻¹y)/dy)

=  √(1-y^2) * (d(sin⁻¹y)/dy)

∴ d(sin⁻¹y)/dy = 1/√(1-y^2)

the derivative of cos⁻¹y = -1/√(1-y^2)

d(sin⁻¹y)/dy + d(cos⁻¹y)/dy = 0

∴ sin⁻¹y + cos⁻¹y = a costant = π/2

（sin⁻¹y = θ, cos⁻¹y = α, θ + α = 90˚）

P13 Growth rates and log graphs

(本节主要举例讲解log的实际应用：能够更精确地测量出函数中的指数大小（增长率）)

Growth functions:

• linear growth(proportional to x = cx)
• polynomial growth(some power of x, like x^2, x^3...)
• exponential growth(2^x, e^x, 10^x...)
• factorial growth(x!, x^x...)

Decay functions:

1/x, 1/x^2, 1/e^x, 1/x!...

Some practical uses of log scale

example1:

example2:

P14 Two different ways that the derivatives are used

Linear Approximation

• Find f(x)

At x = a, df/dx = f'(a) ≈ (f(x) - f(a))/(x - a)

f(x) ≈ f(a) + (x - a)f'(a)

Example:

find√9.06

- find f(x), when x = 9.06

find e^0.01

f(x) = e^x, f'(x) = e^x

a = 0, f(a) = 1, f'(a) = 1

e^0.01 ≈ 1 + (0.01 - 0)*1 = 1.01

-linear approximation and power series

(f(a) + (x - a)f'(a) + ...不断逼近f(x), 下一项是(1/2)(x-a)^2*f''(a))

Newtone's Method

• Solve F(x) = 0 (find x)

At x = a, df/dx = F'(a) ≈ (F(x) - F(a))/(x - a)

x - a ≈ -F(a)/F'(a)

Example:

find√9.06

- when x = √9.06, x^2 - 9.06 = 0 = F(x)

F(x) = x^2 - 9.06 = 0, F'(x) = 2x

choose a = 3, F(a) = 3^2 - 9.06 = -0.06, F'(a) = 2*3 = 6

x - 3 ≈ 0.06/6 = 0.01, x ≈ 3.01

the 2nd cycle of newton's method - closer to the the x(solution)

choose A = 3.01, F(A) = 3.01^2 - 9.06 = 0.0001, F'(A) = 2A = 6.02

x(new) - 3.01 = -0.0001/6.02 = 3.009983...

x(new)^2 = 9.060000001 - extremely close to the x(solution)

P15 Power Series and Euler's Great Formula

Taylor series

Construct the power series:

f(x) = a0 + a1x + a2x^2 +a3x^3 + ... + anx^n

find an = ?, match at x = 0, anx^n = nth derivative of f(0)

• f(0), f'(0), f''(0), f'''(0), ..., nth derivative of f(0)
• nth derivative of nx^n = n!

e^x = 1 + x + (1/2)x^2 + (1/6)x^3 + ... + (1/n!)x^n

• match at x = 0, (e^0)''' = (e^0)'' = (e^0)' = e^0 = 1

f(x) = sinx = x - (1/3!)x^3 + (1/5!)x^5 - (1/7!)x^7 + ...

• f(x) = sinx, f'(x) = cosx, f''(x) = -sinx, f'''(x) = -cosx, f''''(x) = sinx, ...
• match x = 0, f'(0) = 1, f''(0) = 0, f'''(0) = -1, f''''(0) = 0, ...
• f(x) = a0 + a1x + a2x^2 +a3x^3 + ... + anx^n
• a0 = 0
• (a1x)' = f'(0) = 1, a1 = 1
• (a2x^2)'' = f''(0) = 0, a2 = 0
• (a3x^3)''' = f'''(0) = -1, a3 = -1/6

f(x) = cosx = 1 - (1/2!)x^2 + (1/4!)x^4 - ... (even power)

Euler's Great Formula

geometric series: 1/(1-x) = 1 + x + x^2 + x^3 + ..., |x| < 1

f(x) = 1/(1-x), f' = 1/(1-x)^2, f'' = 2/(1-x)^3，f''' = 3!/(1-x)^4

nth derivative of f(x) = n!/(1-x)^(n+1)

nth derivative of f(0) = n!

a0 = 1

(a1x)' = 1, a1 = 1

(a2x^2)' = 2a2x = f''(0) = 2, a2 = 1...

∴1/(1-x) = 1 + x + x^2 + x^3 + ...

∫(1/(1-x)) = -ln(1-x)= x + (1/2)x^2 + (1/3)x^3 +..., |x| < 0

P16 Differential Equations of Motion(eg. spring)

Example：

1、r = 0, F = ma

2、my'' + 2ry' + ky = 0

try y = e^λt , mλ^2 +2rλ + k = 0, λ = ( - r ± √(r^2-km))/m

（1）1y'' + 6y' +8y = 0, y = Ce^(-2t) + De^(-4t)

（2）1y'' + 6' + 10y = 0, y = Ae^(-3t)cost + Be^(-3t)isint

（3）1y'' + 6y' + 9y = 0, y = Ce^(-3t) + Dte^(-3t)

Conclusion：

P17 Differential Equations of Growth

dy/dt = Cy + S

P18 Summary

6 functions

• (x^(n+1)/n+1- x^n  - n*x^(n-1)
• -cosx - sinx - cosx
• cosx - -sinx
• (e^cx)/c - e^cx - c*e^cx
• xlnx -x - lnx - 1/x
• δ function

6 rules

• af(x) + bg(x) - af' + bg'
• f(x)g(x) - f(x)*g' + g(x)*f'
• f(x)/g(x) - (g(x)*f' - f(x)*g')/(g(x)^2)
• x = f⁻¹(y) - dx/dy = 1/dy/dx
• chain rule = f(g(x)) - (df/dy)*(dy/dx)
• L' rule

6 Theorems

what are these mathematical symbols called in English

• f(t) is called "f of t", t is an input, f(t) is an output
• x^2 is called "x squared"
• e^x is called "e to the x", e^0.01: "e to the power point o one"
• n！= n factorial
• e is called Euler's number
• if a function is symmetric across 0: f(x) = f(-x), it is called an even function
• if a function is anti-symmetric across 0, it is called an odd function
• cos⁻¹ is called arc-cosine

Math glossary

calculus 微积分

function 函数

slope 斜率

algebra 代数

differential calculus - from f(t) to df/dt 微分学

integral calculus - from df/dt to f(t) 积分学

formula 公式

parabola 抛物线

derivative 导数（金融衍生品）

the second derivative 二阶导数

convex and concave curves 凸函数和凹函数

inflection point 拐点

cubic/quadratic/linear 三次方/二次方/直线

exponential equation 指数方程

factorial 阶乘

binomial theorem 二项式定理

geometric series/ progression: 1+x+x^2+x^3+...+x^n 几何级数：当x<1，几何级数趋向收敛；当x >=1，几何级数趋向 ∞

least squares 最小二乘法

trapezoid 梯形

square root 根号

epsilon = ε

delta = δ

radian 弧度

fraction 分数

symmetric 对称的

logarithm 对数

proportional to x = cx