高中数学基础与解法全集(涵盖所有)|长期更新|从零开始拯救所有学渣!通俗易懂|高

(包含必修二、选择性必修一、选择性必修二)
必修一
第一章.集合(后面学习时候容易忘记的点稍提一下)
空集是任何集合的子集
必修二
第五章.三角函数

单位圆

二次式往一次式靠 “1”

两种画图方法

cotx图像

公式合集 背

换元法:对形式不清楚时,整体换元

三角函数综合:二倍角转换(熟练)

满足【0,兀】上恰好取一次最大值 兀在第一个最高点右边,兀在第二个最高点的左边

第六章.平面向量
角平分线考虑正弦定理
中线考虑余弦定理

sin角与边的转换


三角形存在 a+b>c
大角对大边
保证为锐角三角形 cosC>0 余弦定理转化为边的关系

通过正弦定理约去相同sin值
边换角 角换边
在三角形ABC中 sinA=sin(B+C)

正弦定理出现和差角公式

基本不等式模型
第七章.复数

复数的三角形式

’表示复数乘积辐角

表示复数除法辐角

| |在复数中是模,不要忘记平方后开根
第八章.立体几何(前部分)
分类

第九章.统计

第p百分位数
第一四分位数:25%
Σ求和方式


总身高的两种表达方式
第十章.概率
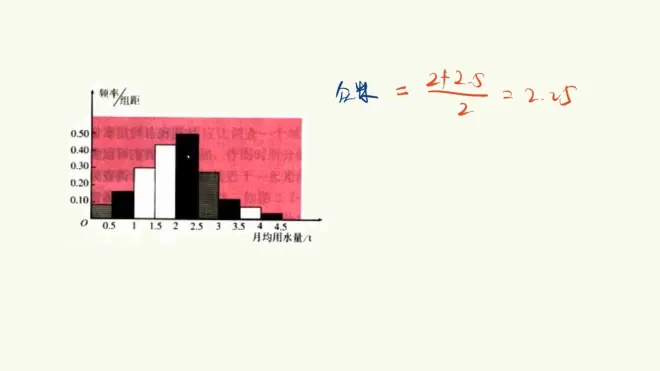
众数求解方法
标准差=方差开根

茎叶图 适用于两个 之间的比较
样本空间&事件

子集

样本之间的关系

步骤
第八章.立体几何(续)

三视图

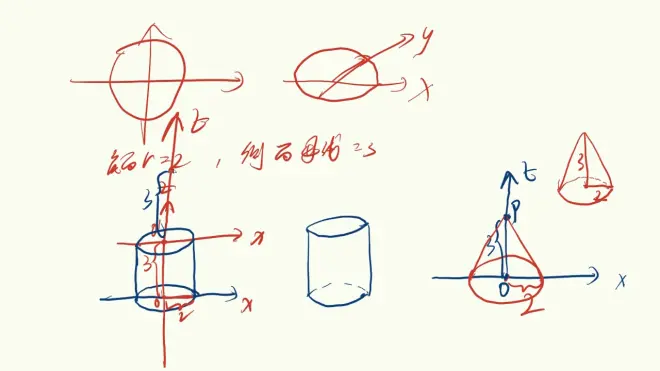
地面圆画为椭圆

棱柱棱锥棱台V S

圆柱圆锥圆台 V S
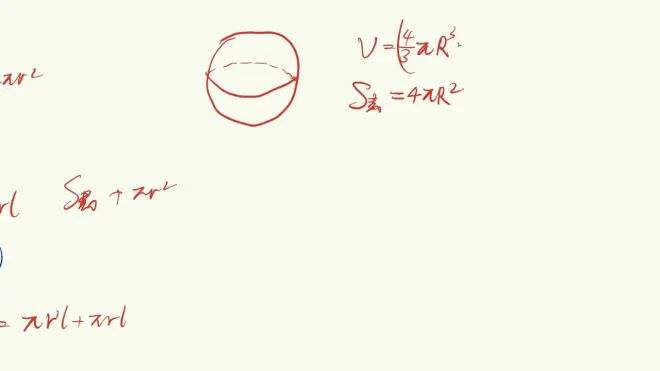
球V S

寻找地面r与母线l的关系

基本不等式你(三元)

例题

例题
动态图
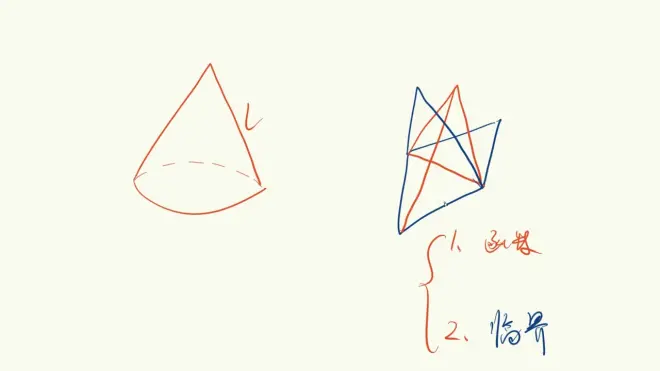

最值问题化不等式
公理






直线关系

两线夹角

异面直线夹角(锐角或夹角)
直线与平面的关系

夹角


夹角计算方式:做平行线平移
(插入)
线面平行 判定定理

线面平行 性质定理

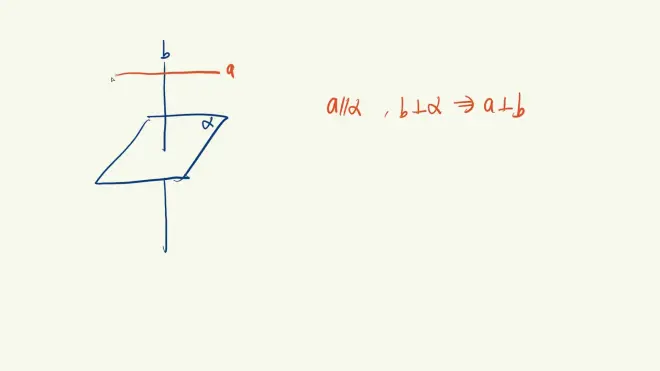
面面平行 判定&性质

(插入) 外接球之墙角模型
补全


转换成墙角模型 )
居然看到这了!
那就投个币吧!
必修二
第一章.空间向量

和平面向量一模一样


通过找法向量之间的关系找线 面各种关系
看到三线两两垂直,建立坐标系
(万能法向量)

求二面角sin值,根号|1-cos方 |

求法向量:找平面内的两个相交直线,相乘为0


把底面画出来,方便分析


画出俯视图


空间向量建系

(复习)

面面: cos阿尔法 正 面面钝角,
cos阿尔法 负 面面锐角
例题
第二章.直线和圆的方程

斜率 倾斜角 :大于等于0度小于180度

阿尔法与斜率的关系



直线的方程
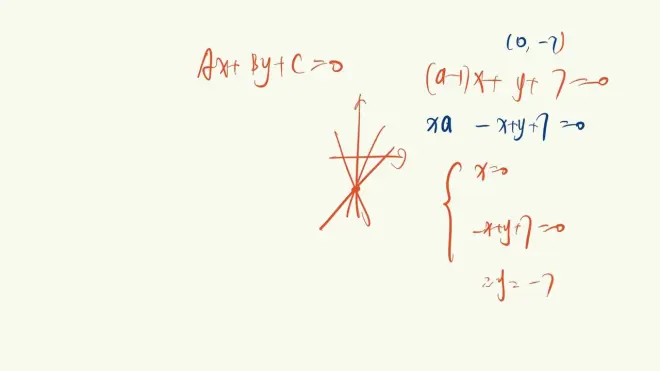
含参直线横过定点
圆的标准方程,一般方程



直线和圆的方程

圆和圆的方程

点到直线距离公式

例题 解答



k与0(theta)的关系 k不能取0

例题

以a为参数,将前面系数变为0

例题

根据垂直和平分列出两个方程求解

将军饮马模型

关于原点对称

第三章.圆锥曲线方程
椭圆方程


例题

例题1

例题2

找直角三角形建立方程

没说a大于b的情况下要进行分类讨论
双曲线
(含绝对值只含双曲线的其中一条)

渐进线

例题


例题 :焦点三角形


抛物线

p指的是焦点到准线的距离,永远大于0
开口向左向右,此时抛物线不是函数
X方向与Y方向分别列式求解

利用90度和抛物线定义

垂线,相似,中位线

两圆半径之和之差

x轴上的点不能取到

椭圆常见题型

利用中点

角度求解

将sin转化为tan

建立方程


点差法 斜率和中点

例题


这一讲认真听
椭圆小题
利用内心列方程





(重复听)
双曲线题目 :设r求出各个线段列勾股定理




抛物线问题 :线段转换

平方平均数和算术平均数

弦长公式


设反式 不用讨论k不存在的情况(与x轴垂直)



大题中的垂直翻译

weida定理+设反式不用讨论k不存在的情况
(与x轴垂直)

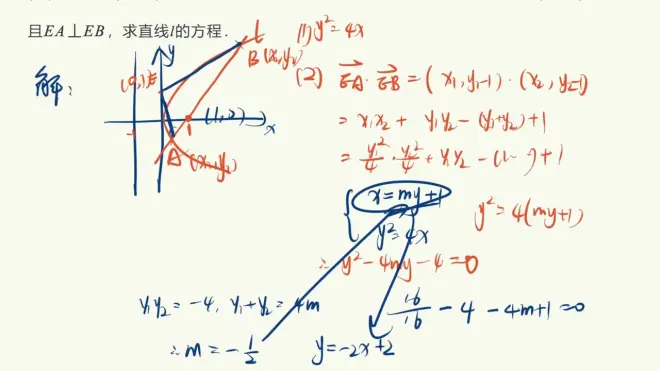
垂直平分与对称问题


点差法)

大题中的点差法

例题
(1)易错:C不能在y轴上即x不等于0
(2)设反式不用讨论k不存在的情况
(与x轴垂直)且此题直线不会平行于x轴


两个角相加等于某一定角
将tan视为倾斜角



大题中角相等的问题


斜率,坐标,联立

轨迹问题
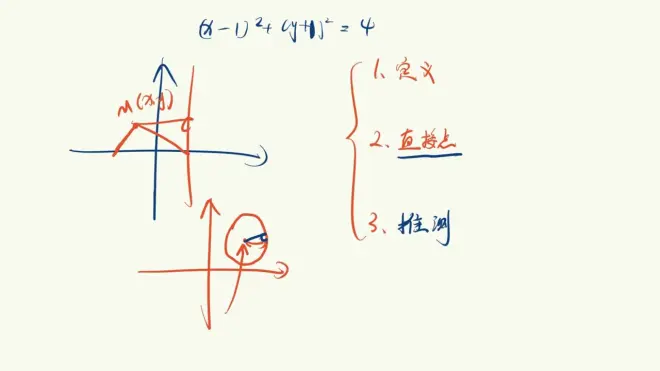



引入未知数,直接设点
居然看到这了!
那就投个币吧!
选择性必修二
第四章.数列


一般情况下没有a0除非题目有表示

利用(-1)的n次方进行调配
数列逆推

等差数列,公差,中项

等差数列 通项公式


等差数列的求和公式

例题

此类题,看a与0的大小关系
题目

不知道是等差数列,需要去求证
反解bn


Sn最小正整数值

利用通项公式

等比数列

通项公式
等比数列的公比q不能为0
q=1时为常数列
等比数列a,b,c满足b方=ac


小题

Sn的通项公式 (错位相减)

题目

累加法 等差数列


差值为指数 也可用累加法

累乘法 等比数列


待定系数法
常数


指数



通项公式与等差数列等比数列的关系
等差

等比

题目(等差)

小题(等差)

小题(等比)

An Sn混搭
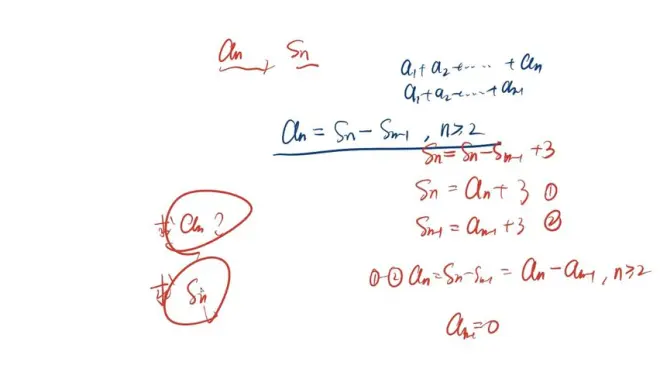
求什么,就把另外一个约掉

待定系数法
题目

判断Sn不为0


数列求和 错位相减


一般形式 (重点)

裂项相消法,数列求和

技巧

保证n前面的系数相等(之后方便约掉)
根号形式

+k后 差多少补多少

三项

题目


倒序相加

分组求和
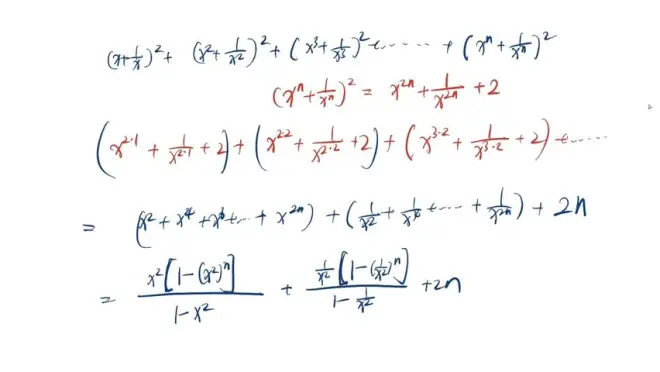

注意:n=正负1的时候能否符合条件
第五章.导数
类比物理知识
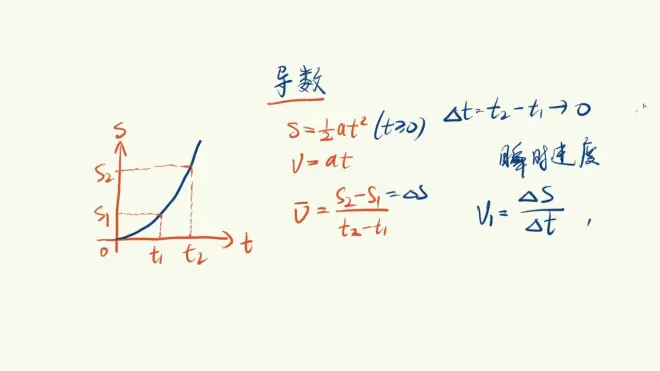


小题


将x=2带入

导数的概念与求导

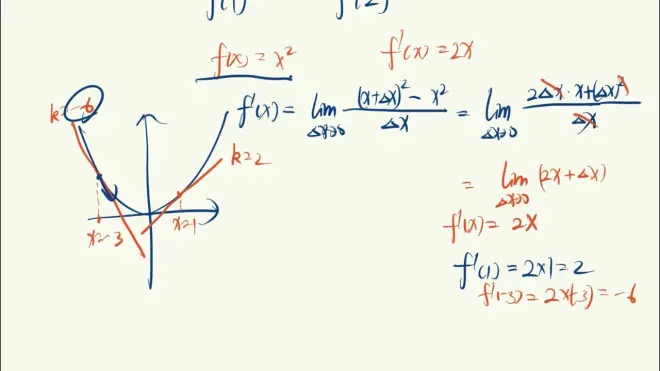
公式(重点)

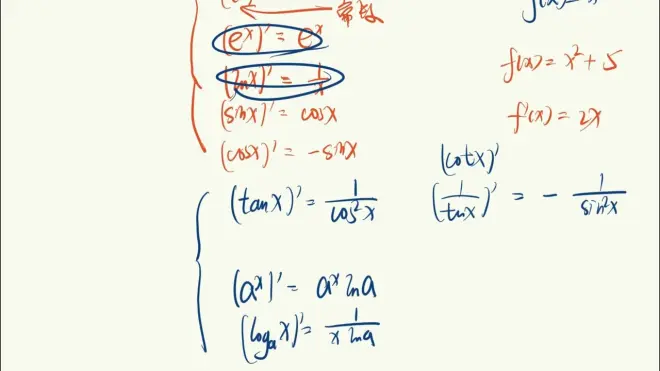
例题 (左侧)
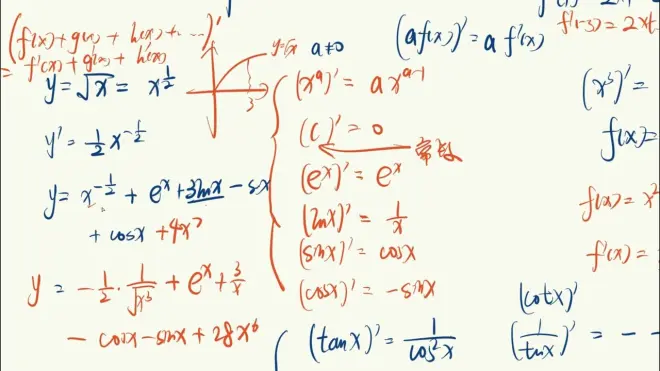
导数运算
相乘

相除

复合函数求导 符合链式法则

右下:对x求导还是对f(x)求导
三层 把里面的数当成整体u,求导

导数运算习题课
小题 两个函数相乘的求导运算

这里的f(Π/6)不是函数,是值


函数的单调性

极值与最值

极小值: 下降趋势的终结,上升趋势的开始

y=X三次方 的原点不是极值点
最大值:极大值或者端点

居然看到这了!
那就投个币吧!

