立体几何

一、基本立体图形

（一）空间几何体

1. 多面体

• 棱柱：所有侧面都是平行四边形

  （1）平行六面体是单独的定义，它既可能属于斜棱柱，也可能属于正棱柱

• 棱锥：

  （1）每个侧面都是三角形

• 棱台：

  （1）上底面与下底面相似，且延长线汇于一点

2.旋转体（母线有无数条）

• 圆柱

• 圆锥：所旋转的三角形底边要与旋转轴呈直角

-----------------------------------------------------------------------------------------

例1

-----------------------------------------------------------------------------------------

例2

—————————————————————————————

二、立体图形的三视图

• 正视图（主视图）

• 侧视图（左视图）：从左往右看

• 俯视图

-----------------------------------------------------------------------------------------

例1

-----------------------------------------------------------------------------------------

例2

-----------------------------------------------------------------------------------------

例3

—————————————————————————————

三、立体图形的直观图

• 斜二测画法是用于画平面图形的。画法：

  （1）x长度不变且平行不变（与x轴平行的线都不变）

  （2）y长度减半且平行不变

• 画圆时，省略y轴，画成椭圆即可
  

————————————————————————————

四、简单几何体表面积与体积

1. 长方体体积=长·宽·高

-----------------------------------------------------------------------------------------

例1

-----------------------------------------------------------------------------------------

例2

• 菱形的面积=对角线乘积的一半
  

2. 棱柱可以歪，圆柱必须直

锥体的顶点作底面垂线，垂足必为底面圆心

-----------------------------------------------------------------------------------------

例3

————————————————————————————

五、几何体的结构问题

-----------------------------------------------------------------------------------------

例2

• 几何平均数永远算术平均数

-----------------------------------------------------------------------------------------

例3

• 正四棱锥：底面为正方形，侧面为全等的等腰三角形，过上顶点做下底面的垂线，垂线一定是下底面的中心

————————————————————————————

六、几何体的展开问题（最短路径）（需再看一遍正余弦定理）

-----------------------------------------------------------------------------------------

例1

• why 角度为90°？

-----------------------------------------------------------------------------------------

例2

-----------------------------------------------------------------------------------------

例3  ？？？

• 正弦定理求三角形面积：

-----------------------------------------------------------------------------------------

例4

————————————————————————————

七、动态图形探究

1. 动态图形的最值问题

• 把运动过程中体积、面积函数表示

• 临界情况

-----------------------------------------------------------------------------------------

例1

-----------------------------------------------------------------------------------------

例2

• 等腰三角形三线合一

• 平方差公式：a² - b² =(a-b) (a+b)
  

-----------------------------------------------------------------------------------------

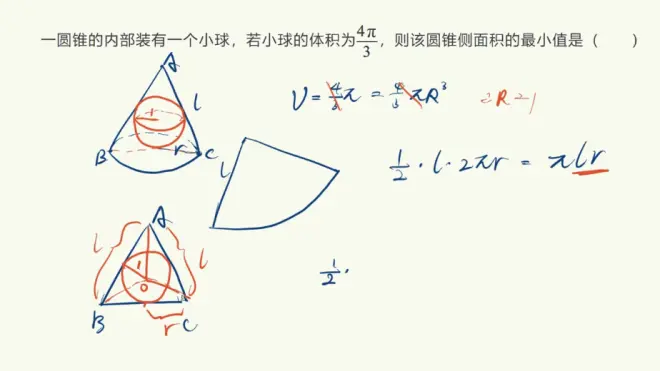
例3 临界值

• 余弦定理：cosA=（b²+c²-a²）/2bc