关于缺项三次方程的一种特别解法

这个问题的研究来源于笔者在一道物理题目中遇到的障碍，完全简化之后即为一个简单的三次方程:

x³+3x-2=0

。由于其的实根形式比较复杂，无法一眼看出结果，而用卡丹公式求解计算又显暴力，于是笔者思考:是否可以用三角函数的三倍角公式求解？

笔者的第一想法当然是不能。对于

cos3θ=4cos³θ-3cosθ

和

sin3θ=3sinθ-4sin³θ

，此方程的三次项和一次项同号，又怎么能配凑系数呢？然而笔者同学大胆提出了配凑复系数的想法，于是笔者进行了如下尝试:

(某些术语措辞极不严谨，实际上笔者水平不高，见谅)

对于我们最后得出的两个解族，笔者尝试化简，但努力许久未能成功。笔者只好借助现代科技的力量观察结果

(图中p=0)

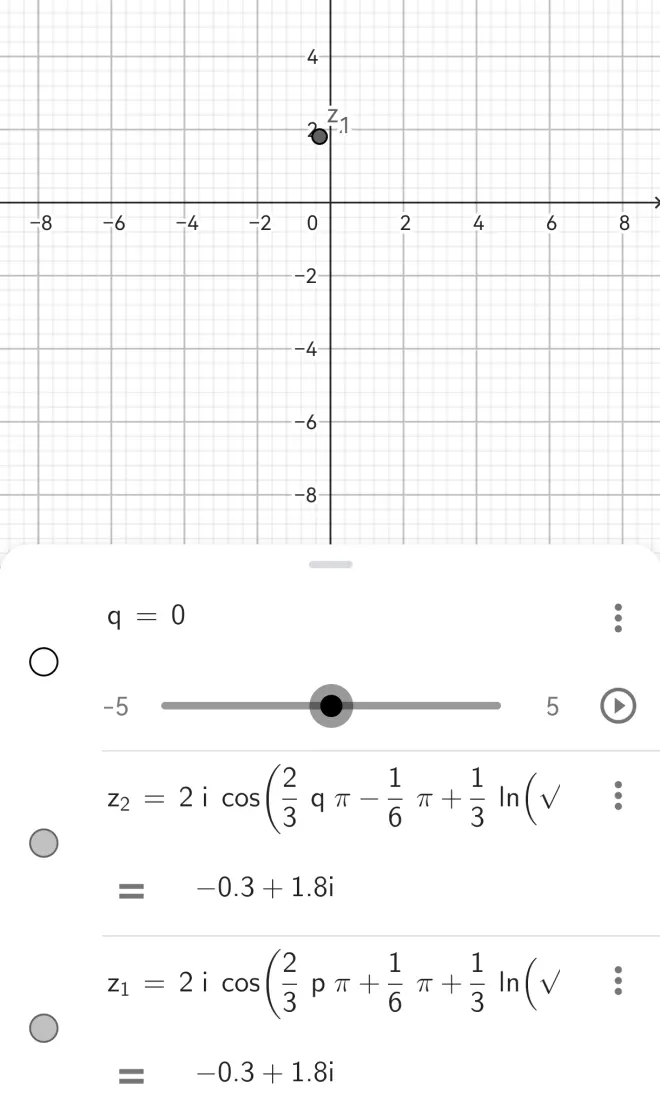
我们惊奇地发现，当p=q=0时，z1=z2。而继续探究后可知，实际上z1z2的轨迹是重合的，

也就是说这两个解族本质上是同一个!

(由于k为整数 这句话并不严谨 笔者只表达大概)

虽然笔者的化简工作已经减少了1/2，但仅仅如此远远不够。笔者继续观察了此方程的一个实数根与两个复数根。当k=-1，我们的解是一个实数，即上图中x1

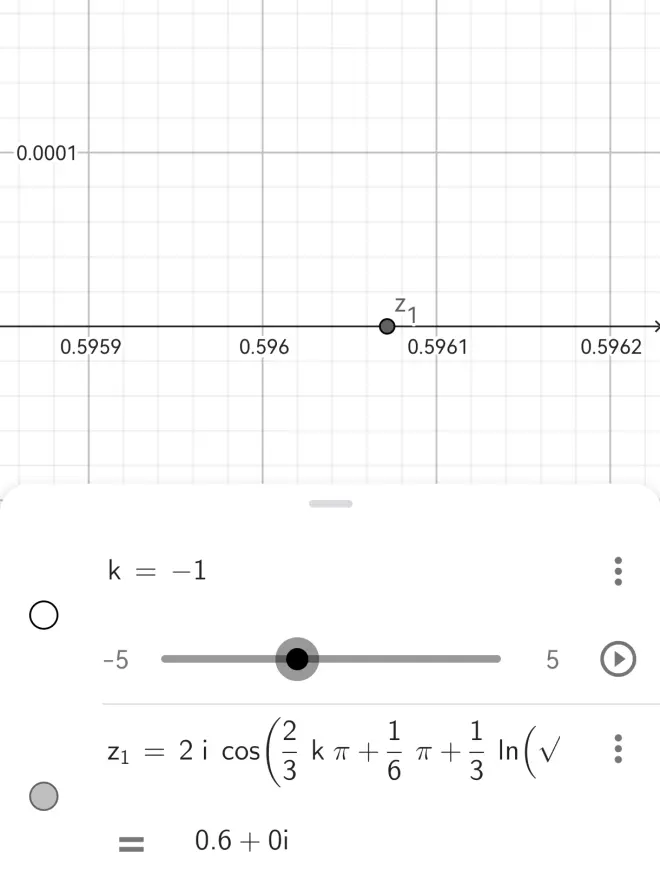
聪明的朋友已经发现了，当k取不同的整数值，理论上可以得到x2和x3，这里就可以开始推广成全体缺项三次方程甚至三次方程的解法了。但是我们并不着急，实际上我们的最终结果可以进一步化简

(愚蠢的笔者并没有意识到一开始就可以对结果用和角公式 探究了很久)

正如我们所见，最终得到了一个形式较为简约的根形式

于是笔者开始思考:能否将此方法推广到全体缺项三次方程？

经过一番搜索，笔者发现了此法的本质——

双曲函数

如图中的sinh(x)即是双曲正弦函数。关于双曲函数定义，可以搜索了解(

其实是笔者也不太懂

)

sinh(x)=(eˣ-e⁻ˣ)/2

cosh(x)=(eˣ+e⁻ˣ)/2

我们会发现双曲函数与欧拉公式得到的三角函数非常相似 即

sinx=[e^ix-e^(-ix)]/2 cosx=[e^ix+e^(-ix)]/2

。借助双曲函数，我们可以简易地表达最终的结果:

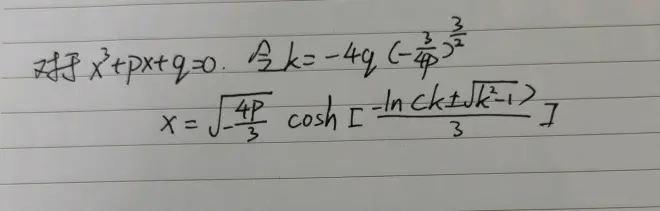
(推导过程类似笔者第一次尝试的书写，即图2。先配凑复系数成三倍角公式然后利用欧拉公式求解)

至此，我们已基本完成了双曲函数对缺项三次方程的解法。而我们熟知，完整的三次方程可以通过换元配凑成缺项三次方程，于是这种方法就推广到了全体的三次方程。

笔者第一次看到方程x³+3x-2=0就因为系数否定了配凑三倍角的想法，但在尝试中，笔者发现了一个从未见过的领域。大胆探索，小心验证，往往就是数学魅力所在OAO

感谢观看