6.5 小批量梯度下降法

2023-02-22 10:43 作者:梗直哥丶 0人读过 | 我要投稿

前面几节介绍了批量梯度下降法和随机梯度下降法，各有问题。前者计算量大速度慢，后者容易出现搜索中的震荡情况。于是科学家们很自然的就想找个折中方案，这就是小批量随机梯度下降法（Mini-Batch Stochastic Gradient Descent）。本节咱们就来具体看看它的基本原理和各种特点。

6.5.1 基本思想

小批量随机梯度下降法的基本思路是在每一次迭代中，使用一小部分的随机样本来计算梯度，然后根据梯度来更新参数的值。它的基本流程如下：

6.5.2 优缺点

6.5.3 代码比较

我们用一个例子来演示三种梯度下降法在代码实现上的异同。在下面这个例子中，我们使用 PyTorch 中的 torch.optim.SGD 函数来创建优化器。通过设置 momentum 参数为

来使用随机梯度下降法，设置为非

值则使用常规的梯度下降法。批量大小设置为

，这意味着每次更新模型参数时使用了

个样本。当然可以根据需要调整批量的大小，以获得最优的训练效果。特别注意的是，下面这个例子重点是为了演示三种算法在代码实现上的区别，简便起见，我们使用了随机生成的数据来训练模型。损失值的变化趋势的结果可能会因为训练数据的不同而有所差异。

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from tqdm import *

# 定义模型和损失函数
class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden1 = nn.Linear(1, 32)
        self.hidden2 = nn.Linear(32, 32)
        self.output = nn.Linear(32, 1)

    def forward(self, x):
        x = torch.relu(self.hidden1(x))
        x = torch.relu(self.hidden2(x))
        return self.output(x)
loss_fn = nn.MSELoss()

# 生成随机数据
np.random.seed(0)
n_samples = 1000
x = np.linspace(-5, 5, n_samples)
y = 0.3 * (x ** 2) + np.random.randn(n_samples)

# 转换为Tensor
x = torch.unsqueeze(torch.from_numpy(x).float(), 1)
y = torch.unsqueeze(torch.from_numpy(y).float(), 1)

# 将数据封装为数据集
dataset = torch.utils.data.TensorDataset(x, y)

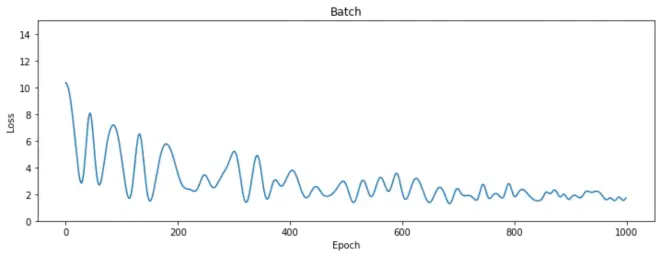
names = ["Batch", "Stochastic", "Minibatch"] # 批量梯度下降法、随机梯度下降法、小批量梯度下降法
batch_size = [n_samples, 1, 128]
momentum= [1,0,1]
losses = [[], [], []]

# 超参数
learning_rate = 0.0001
n_epochs = 1000

# 分别训练
for i in range(3):
    model = Model()
    optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, momentum=momentum[i])
    dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size[i], shuffle=True)
    for epoch in tqdm(range(n_epochs), desc=names[i], leave=True, unit=' epoch'):
        x, y = next(iter(dataloader))
        optimizer.zero_grad()
        out = model(x)
        loss = loss_fn(out, y)
        loss.backward()
        optimizer.step()
        losses[i].append(loss.item())

# 使用 Matplotlib 绘制损失值的变化趋势
for i, loss_list in enumerate(losses):
    plt.figure(figsize=(12, 4))
    plt.plot(loss_list)
    plt.ylim((0, 15))
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.title(names[i])
    plt.show()

Batch: 100%|██████████| 1000/1000 [00:07<00:00, 129.91 epoch/s]
Stochastic: 100%|██████████| 1000/1000 [00:00<00:00, 2397.32 epoch/s]
Minibatch: 100%|██████████| 1000/1000 [00:01<00:00, 780.15 epoch/s]