原文链接：http://tecdat.cn/?p=11803 

Nelson-Siegel- [Svensson]模型是拟合收益曲线的常用方法。它的优点是其参数的经济可解释性，被银行广泛使用。但它不一定在所有情况下都有效：模型参数有时非常不稳定，无法收敛。

纳尔逊（Nelson）和西格尔（Siegel）在其原始论文中从远期利率入手，然后推导了收益率至到期曲线的公式.

Nelson-Siegel模型是简约的，可以生成丰富的收益曲线。

但是，由于简单地使用它，它通常失去了经济上的可解释性，甚至无法收敛。

上图显示了这种情况。

1. 


2. plot(MATURITY_BASES, oldYields

3. lines(MATURITY_BASES, oldYields)

4. points(newMats, newYields, col="blue")

5. lines(newMats, newYields, col="blue")

此代码模仿了一个频繁使用的案例，当前的收益曲线与昨天的曲线进行了比较。从某种意义上讲，这是一个简单示例，因为对于给定的到期日，我们已经具有零收益率。实际上，我们通常与票息债券有关，这会使事情变得更加复杂。

您可能会认为，由于软件的实施而导致收敛失败。我要讲的不是不好的实现，而是要高度依赖所使用的数值方法，如下面的更实际的示例所示。

提供更逼真的建模

1. #include <ql/qldefines.hpp>

2. #ifdef BOOST_MSVC

3. #  include <ql/auto_link.hpp>

4. #endif

5. #include <ql/termstructures/yield/fittedbonddiscountcurve.hpp>

6. #include <ql/termstructures/yield/piecewiseyieldcurve.hpp>

7. #include <ql/termstructures/yield/flatforward.hpp>

8. #include <ql/termstructures/yield/bondhelpers.hpp>

9. #include <ql/termstructures/yield/nonlinearfittingmethods.hpp>

10. 


11. 


12. using namespace QuantLib;

13. 


14. int main(int, char*[]) {

15.     try {

16.         Calendar calendar = NullCalendar();

17.         Date today = Date(18, December, 2017);

18.         Settings::instance().evaluationDate() = today;

19. 


20.         //市场数据

21.         double cleanPrices1[] = { 107.96, 135.88, 110.6,   133.46, 135.8,  142.155, 121.045, 134.97, 117.04,

22.             101.61, 128.67, 106.615, 106.36, 99.515, 101.21,  105.655, 114.828 };

23.         double cleanPrices2[] = { 107.9,  134.965, 110.37,  132.89, 135.62,140.845, 120.585, 133.995, 116.745,

24.             101.58, 128.115,105.985, 105.395,99.385, 100.79,104.955, 114.7985 };

25.         double cleanPrices3[] = { 107.96, 134.625, 110.58, 132.65, 135.145, 140.585, 120.385, 133.735, 116.635,

26.             101.62, 127.925, 105.6, 105.085, 99.29, 100.6, 104.945, 114.7415 };

27.         double cleanPrices4[] = { 107.78, 134.39, 110.175, 132.445, 134.905, 139.515, 120.115, 133.475, 116.455,

28.             101.58, 127.845, 105.53,104.805, 99.07, 100.46, 104.885, 114.6225 };

29. 


30. 


31.         std::vector<boost::shared_ptr<BondHelper> > bondHelpersA;

32.         std::vector< boost::shared_ptr<SimpleQuote> > quoteA;

33.         std::vector<boost::shared_ptr<BondHelper> > bondHelpersB;

34. 


35.         for (Size i = 0; i < numberOfBonds; i++) {

36.             boost::shared_ptr<SimpleQuote> cp1(new SimpleQuote(cleanPrices1<em class="d4pbbc-italic"></em>));

37.             quoteA.push_back(cp1);

38.             boost::shared_ptr<SimpleQuote> cp2(new SimpleQuote(cleanPrices2<em class="d4pbbc-italic"></em>));

39.             quoteB.push_back(cp2);

40.             boost::shared_ptr<SimpleQuote> cp3(new SimpleQuote(cleanPrices3<em class="d4pbbc-italic"></em>));

41.             quoteC.push_back(cp3);

42.             boost::shared_ptr<SimpleQuote> cp4(new SimpleQuote(cleanPrices4<em class="d4pbbc-italic"></em>));

43.             quoteD.push_back(cp4);

44.         }

45. 


46.         RelinkableHandle<Quote> quoteHandleA[numberOfBonds];

47. 


48. 


49. 


50.         //Nelson-Siegel模型拟合

51.         Real tolerance = 1.0e-14;

52.         Size max = 10000;

53. 


54.         boost::shared_ptr<FittedBondDiscountCurve> tsA(

55.             new FittedBondDiscountCurve(curveSettlementDays,

56.                 calendar,

57.                 instrumentsA,

58.                 ActualActual(),

59.                 NelsonSiegelFitting(),

60.                 tolerance,

61.                 max));

62. 


63. 


64.         boost::shared_ptr<FittedBondDiscountCurve> tsB(

65.             new FittedBondDiscountCurve(curveSettlementDays,

66.                 calendar,

67.                 instrumentsB,

68.                 ActualActual(),

69.                 NelsonSiegelFitting(),

70.                 tolerance,

71.                 max));

72. 


73.         boost::shared_ptr<FittedBondDiscountCurve> tsC(

74.             new FittedBondDiscountCurve(curveSettlementDays,

75.                 calendar,

76.                 instrumentsC,

77.                 ActualActual(),

78.                 NelsonSiegelFitting(),

79.                 tolerance,

80.                 max));

81. 


82.         boost::shared_ptr<FittedBondDiscountCurve> tsD(

83.             new FittedBondDiscountCurve(curveSettlementDays,

84.                 calendar,

85.                 instrumentsD,

86.                 ActualActual(),

87.                 NelsonSiegelFitting(),

88.                 tolerance,

89.                 max));

90. 


91.         std::cout << tsA->fitResults().numberOfIterations() << std::endl;

92.         std::cout << tsB->fitResults().numberOfIterations() << std::endl;

正式而言，收益曲线每天的变化并不显着，但是模型参数却可以：

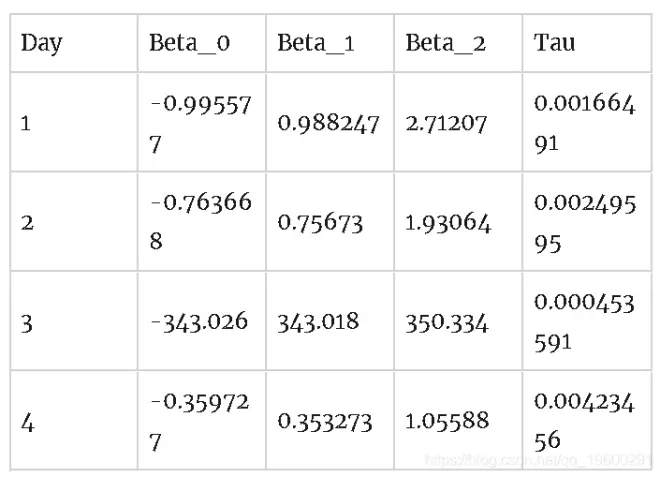
Nelson-Siegel意识到了这些问题，并提供了解决这些问题的方法。特别是，他们考虑了Taus的时间序列，并确定了Taus的最佳拟合值的中值和合理范围。
但是，与往常一样，原始论文被引用的次数可能多于阅读次数。此外，如果需要按时间顺序排列的收益率数据，可能会感到困惑，而不是仅仅考虑相关日期的数据。即使处理时间序列不是问题，Nelson和Siegel也没有指定正式的算法来选择的最佳值。

最受欢迎的见解

1.在python中使用lstm和pytorch进行时间序列预测

2.python中利用长短期记忆模型lstm进行时间序列预测分析

3.使用r语言进行时间序列（arima，指数平滑）分析

4.r语言多元copula-garch-模型时间序列预测

5.r语言copulas和金融时间序列案例

6.使用r语言随机波动模型sv处理时间序列中的随机波动

7.r语言时间序列tar阈值自回归模型

8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类

9.python3用arima模型进行时间序列预测