【编程笔记】高精度算法·加减乘除

高精度的算法思路

1.大整数存储

2.高精度的加减乘除

大整数存储

正常情况下，书写一个数是从高位到低位的，但在高精度中，应该从低位到高位存储。因为对于一个数组来说，从末尾添加数据会比从开头添加数据容易。而在计算中，通常都是从个位数往高位数计算，也就是从计算是不断的往高位数靠的，所以，高位数应该被置于某位。即，对1234而言，a[0]=4，a[1]=3，a[2]=2，a[3]=1。

高精度加法思路

首先，我们令t为进位。a,b为加数和被加数，c为a,b相加后的结果。那么，a为一个大的数组（如1234），a[0]=4，a[1]=3，a[2]=2，a[3]=1。

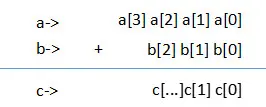
如果a[0]+b[0]<10,那么c[0]=a[0]+b[0]

a[0]+b[0]>=10,那么存在进位，即进位t=a[0]+b[0]的十位数,c[0]=a[0]+b[0]个位数

由于a,b,c均为十进制数，而两位的十进制数=十位*10的1次方+个位*10的零次方。

所以，取进制的方法就是t=(a[0]+b[0])/10,c[0]=(a[0]+b[0])%10

而对c[1]而言，需要加上进位，c[1]=a[1]+b[1]+t

这么一来,可以认为c[i]=a[i]+b[i]+t

高精度加法过程

1.判断加数和被加数进位是否存在，存在便加

2.分别取相加结果之和，取个位压入存储结果的数组，取十位作为进位

3.判断是否存在进位，存在，压入

由于c数组的长度未知，而数组在定义声明时,必须使用常量表达式给出其容量大小,而且程序运行时数组不允许动态的增删元素，vector允许动态的增删元素。故采用vector。

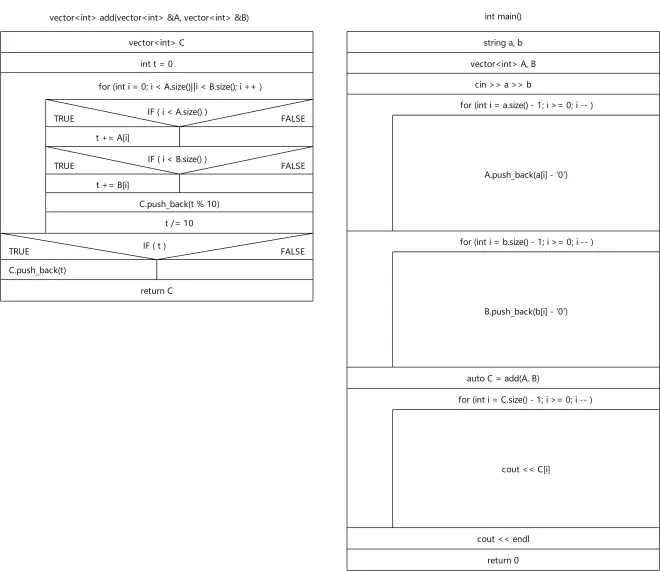
使用vector需要加上#include <vector>

vector相当于一个动态数组，类似于java中的list。

push_back在数组的最后添加一个数据

auto 就是编译器自动判断类型，比如在这里会自动判断为vector<int>(add函数的类型)

a[i]-’0’的目的是将a[i]变成数字，a[i]定义成了字符串来便于输入。

高精度减法思路

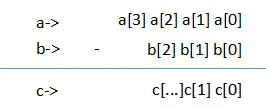
减法与加法之间存在相似之处。

如果a[0]-b[0]>=0，那么不存在问题可以直接相减，即c[0]=a[0]-b[0]。

但如果a[0]-b[0]<0，那么就会出现结果为负的情况，这时候，需要向a[1]进行借位。而与上面相同的是，个位向十位借位就是需要加上10，即c[i]=a[i]-b[i]+10。

同样，从a[1]开始，都存在被借位的可能，因此上述表达式都需要前去借位t

a[0]-b[0]>=0时，c[i]=a[i]-b[i]-t;

a[0]-b[0]<0，c[i]=a[i]-b[i]+10-t;

而对于整个数a,b而言，存在类似的问题。

a-b>=0时，c=a-b;

a-b<0时，c=-(a-b);

最后，还需考虑前导0的问题，即119-110会被视为009，但我们需要的答案是9，所以需要去掉前面的0。在去掉0的时候，还需考虑有1-1=0的情况，这种情况的0是不能被删除的，判断的条件应为c的长度是否为1。

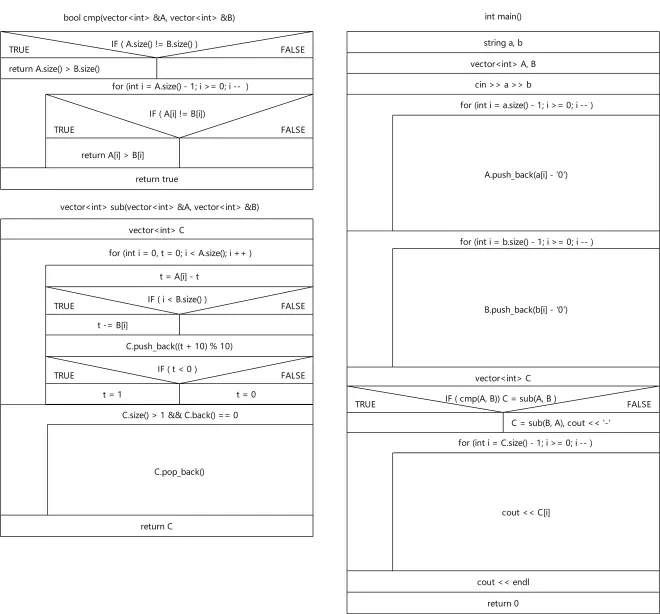
高精度减法过程

1.如果减数和被减数在位置上均有数,带上进位,相减

2.进行借位得到位置上的结果

3.判断是否真的进行了借位来更改借位得值

4.去除前导零

5.比较结果是否大于零,小于零的话,反过来相减并加上负号

高精度乘法思路

整体思想上，高精度乘法和高精度加法相似，这里进行讨论高精度的整数乘以低精度的整数的情况，也就是需要一个高精度的整数乘以低精度的整数。也就是说，不必将b进行大整数存储。

通过加法的思路，可得：

c[0]=(a[0]*b)%10

t=(a[0]*b)/10

c[1]=(a[0]*b+t)%10

t=(a[0]*b+t)/10

可见，乘法在这方面跟加法是一毛一样的。

但是，由于最后的进位存在为零的可能性，需要去除前导零。

高精度乘法过程

1.将每有位数依次和,并加上进位

2.将结果的十位数压入

3.将结果个位数更新为进位

4.去除前导零

高精度除法思路

令c为商，a为被除数，b为除数，r为余数。

由于push_back的压入操作中,是对c[0]往后走的,所以,与大整数存储的思路相反,故还需将整个数的序列进行反转。

乘法与除法的输入输出相同且同样存在前导零的问题。

高精度除法过程

1.通过余数和a[]求新的被除数

2.将新的被除数的十位数压入

3.求余数

4.求出商后,反转序列

5.去除前导零

使用reverse函数需要加上#include <algorithm>。

勤奋，今天的夕弦也很努力呢！