中考结束了，回顾下曾经的网红神题

各省市陆续进入招生录取工作，最近爆出一些神题，都会做吗？今天带大家看看网红中考习题，初二的学弟学妹们，来年就是你们了，加油呀！

“Ⅰ正方形内相互垂直的3条线段及长度如下图，求正方形的面积

分析：怎样可以求出正方形面积？容易想到求边长，看到题目边长好像很难求得，没有邻近关系，求出对角线也行啊，已知条件都在对角线旁绕圈圈，还有一些人想到面积拼接，如果能拼好一定事半功倍，但目前没找到太好拼接办法，求面积比较复杂，我从来不排斥暴力解答，毕竟考试时间有限，可能就是想不到最简单的方法，先来个暴力的吧，随便找一种拼接的方法画辅助线，如下：

方法1：设HC=AG=x，正方形边长为a，面积为s，由于∠HAE=∠DHC，正切值相等，那么有

由②得

由③、④得

由①、④、⑤得

49a^2= 2(a^2-25)^2 -70(a^2 - 25) + 35^2

49s= 2(s- 25)^2 -70(s - 25) + 35^2

2(s -25)^2 -70(s - 25) – 49(s – 25)=0

由根与系数关系，知

那么正方形面积为84.5

如果没能列出可解的拼接算式，那么可以采取如下方法

方法2：如图，设EG长为x，由于AE∥CF，可以根据相似三角形关系列方程，有

那么AC长为

那么正方形面积为13·13÷2=84.5

最不好想的辅助线是作在外面的，只要做出来，就一目了然

方法3：如图，在△AHC中，∠H是直角，根据勾股定理，得AC长为

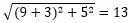
那么正方形面积为13·13÷2=84.5

“Ⅱ网红神题很受欢迎，有出题人把条件改改，同样求正方形面积，成了这样

这题跟前面是一样的，开发思路再介绍个拼接的方法

方法1：可算得BH=DG=10.5cm，根据对称性，知点O为HG的中点，那么BO长为

那么正方形面积为

当然，这题也可以接连接对角线来计算

方法2：如图，根据相似比例有

对角线长为

那么正方形面积为

同理仿效前面用到的拼接方法，也可以这样做

方法3：设BH=DG=x，正方形边长为a，面积为s，同理∠HBC=∠DGC，余切值相等，那么有

由②得

由①、③、④得

由根与系数关系，得

因此正方形面积为225

“Ⅲ当然这题也可以用前面一目了然的辅助线作法，有兴趣的朋友自己完成吧，这类问题添加辅助线至关重要，但有些朋友就是想不到漂亮的辅助线，就得多多练习了，再有就是紧急情况只能列方程计算了，考试时间不足，第一感觉列出的算式可能不是最简单的，计算量大些，但认真完成还是没有问题的，就需要加快计算速度了。还有一点，前面设了两个未知数，那就应该有两个不同的方程式才能得到答案，有些同学列了两个等价的方程，得不到解，怎样才能写出不同的方程式呢？告大家一个规律，列出线性无关的式子就有解——迷糊不，啥样才是线性无关呢？简单来说就像前面列的方程，一个x与水平的a有关，一个x与竖直的a有关，这样两个式子一定线性无关，肯定能得出结果，就是找两个不同性质的关系才可以，这道题很有意义啊。

  最后祝即将中考的同学蒸蒸日上，赢得最后的胜利！