数学实现信号分析 [6]: 窗口傅里叶变换WFT

之前的专栏讨论了连续傅里叶变换和离散傅里叶变换

我们可以发现傅里叶变换有一个缺点:  那就是必须对全部的已有数据进行分析,  并且单独一个数据的改变也会影响整个傅里叶变换的结果

为了可以对一小部分的数据进行分析, 于是就出现了窗口傅里叶变换(Window FT), 或者叫做短时傅里叶变换(Short Time FT, STFT) 或 Gabor变换

时窗函数

为了实现WFT的短时性, 最直接的方法就是把需要分析的那一段信号单独拿出来,  而且既然是分析频率, 那么也不可能只单独拿一个点进行分析, 而需要持续一段时间的信号

提取信号的方法就是构造一个函数, 在趋向无穷时快速收敛或直接等于零,   把原信号函数跟这个函数相乘, 就得到了一个仅限于局部的信号函数, 然后再对这个新函数进行分析就好了,  而这个构造出来的函数就叫做时窗函数

那么WFT的表达式为:

其中, GF(ω, t) 为WFT的变换方法,  w(τ-t) 是向右平移了 t 的窗函数,  ω是频率,   而 f(τ)w(τ-t)  是原信号函数在 时刻t 被时窗函数w截取出来部分

其表达式也是非常直接的,  以下使用原函数  f(t) = sin(t^2) , 而窗函数  w(t) = { |t| < 1: 1+cos(t),  others: 0}  为例子:

红色为原函数, 橙色为原函数的傅里叶变换, 可以看到非常混乱, 完全看不出有什么规律, 绿色为窗函数, 蓝色为b0=5时原函数被时窗截取的信号, 紫色就是信号作傅里叶变换的结果, 可以看到刚好在w=5处有一个尖峰, 也就是说我们的窗口傅里叶变换表现得非常好

频窗函数

与时窗函数相同, 有的时候我们需要把一部分频率范围进行逆变换得到这个频率对应的信号

频窗函数与时窗函数只有两点不一样,  第一, 时窗函数必须是实函数 (即在时间t内全部为实数的函数), 而频窗函数可以为复函数 (即在频率ω内可以为复数的函数),  第二, 时窗函数与其自身的内积必须为1, 而频窗函数没有这个要求

高斯窗

在通常WFT中, 数学家们为了追求极致(lan duo), 提出了综合时窗和频窗的窗函数, 对窗函数有以下几点要求:

1. 窗函数在时域中与自身内积为1, 且在时域中为实函数.  2. 窗函数在时域里的定义函数经过傅里叶变换后得到频域定义函数.  3. 窗函数在时域和频域中都具有特定的开窗半径

在符合以上要求的窗函数里, 最简单的就是高斯窗, 也就是用高斯函数作窗,  高斯窗的定义如下***  这个函数貌似是教材里写错了, 这里我自己擅自进行了更改, 详情见下面备注 *** 

高斯窗有一个非常美妙的性质就是: 在经过傅里叶变换后也是实高斯函数

这就意味着高斯窗在通常的情况里是一个非常好的窗函数

时频图

在WFT中我们可以看到有两个变量: 频率ω和时间t, 

如果我们把x轴作为时间, y轴作为频率, 那么就可以对任意一个信号作WFT并记录在图像上

这里使用一首歌作一个例子:

iWFT (逆窗口傅里叶变换)  *********

不知道哪个人说过:  没有逆变换的变换是不存在意义的

所以我这里直接给出逆变换 (虽然我一开始以为是没有逆变换的 = = )

在教材里使用的窗函数是标准高斯函数

这个函数有一个问题, 就是它并不满足窗函数的一个条件:  (在时域内的内积为1),  这个函数在时域内与自身的内积的数值与a有关, 也就是说并不是一个定值

但是这个函数在实数内积分等于一 (当然, 高斯函数嘛),  

如果使用这个函数作窗函数的话, 除了上述这点, 其他地方表现得跟我修正的那个一样好, 除了逆变换

逆窗口傅里叶变换是建立在一个基础上的, 那就是 (在时域内的内积为1), 那么针对这个高斯函数, 逆变换就需要更改为

使用这个式子计算是可以得到准确答案的,  但是!!!  但是!!! 在这个教材里使用标准高斯函数, 但是逆变换是含有w的那个,  我:????

关于逆变换的证明:

窗口傅里叶变换可以看作以下过程:

那么就有:

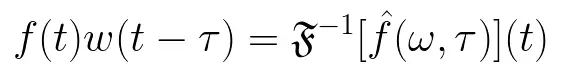
两端同乘一个w再对τ积分有:

右边的式子稍微把F^-1写出来就是逆窗口傅里叶变换的式子了,  而左边我们化简一下得:

Q.E.D.

彩蛋:  下期预告: 不确定性原理