问题：

        1. 我们都知道“单调有界数列必有极限”是判断数列是否收敛的一个重要方法，而数列又是一类特殊的函数，但这个判定直接用在函数上是不成立的。

        2. 对于在实数域R上单调有界的可微函数，是否一定有

虽然直观上看上去好像会有

例如

满足单调、有界，且

还有许多这样的函数，单调有界，连续可微，有

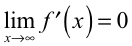
然而由于并没有把所有的满足单调有界、连续可微的函数都列举出来，所以下面Moran在文献[1]提供了一个构造此类函数的思路，范丽君教授在文献[2]中给出了一个具体的反例。

反例

问题1

        首先，“单调有界数列必有极限”，对于这个判别定理，我们具体的知道数列这一特殊函数，其极限过程只有一种，就是n→∞（n默认为自然数），而一般函数极限过程则有多种可能，如x→+∞，x→-∞，x→∞，x→0+等，对于一个函数来说，即使是单调函数，对于不同的极限过程，其极限可能存在也可能不存在。例如

例1. 对于

当x→+∞，x→-∞时

但当x→∞时

极限不存在

例2. 对于函数

我们知道在其定义域内是单调有界函数，x=0是f(x)在其定义区间的一个跳跃间断点，那么尽管函数f(x)在其定义域内是单调有界函数，但当x→0时，其极限也不存在。

问题2

        首先是由Moran提出的构造此类函数的思想方法:

下面是由范丽君教授构造的一个具体的反例：

所以，当我们要用“单调有界原理”应用在函数极限时，需注意只有对于函数的单侧极限才是成立的

参考文献

[1]  Moran, D. A: For a collection of examples and counterexamples, Amer Math Monthly, 68(1061), 508-509.

[2]  范丽君, 郭挺. 一类单调有界光滑函数的导函数极限存在性[J]. 江西理工大学学报, 2010, 31(3): 69-73.