S2E3L6 夏至的日照与杆影变化

2020-06-20 12:59 作者:学用数学 0人读过 | 我要投稿

在夏至中午时，若在北回归线上立竿，这时可就看不到「立竿见影」的效果。在 2015 年夏至时，我就想要进一步了解探究，当改变北纬 23.5° 的位置，改变时间，那杆影长会是如何变化的呢？我当时就带着这个好奇来用 Geogebra 作了这个探究课件。

学习指引

这个课件看起来效果很酷炫，但其实其制作并没有想象中的困难。最关键点就是纬线上动点的控制。其他基本操作就是 Geogebra 的 3 维功能，而对于杆影长比例的显示关键就在于想到建切平面，再取直线的交点来求解。

数学思维

建立一个坐标系来显示圆上的动点

Geogebra 操作指令

平面，垂直面、切平面
向量
显示条件
动态文本

相关基础课程

建议先对以下空间中的基本操作熟悉后再来学些这个专题

平面截正立方体

https://www.bilibili.com/video/BV1va4y1v7xE

平面截圆锥

https://www.bilibili.com/video/BV1s7411X7E1

相关进阶课程

球面上两点距离

https://www.bilibili.com/video/BV1pk4y167d6

任务一：球面的自转轴

【目的】希望建一个自转轴可调整的球面，并显示出太阳照射到的半球与没照射到的半球区域。

参考视频： https://www.bilibili.com/video/BV1u4411P79R?p=3

GGB: https://www.geogebra.org/m/rpvq55df#material/juj2zfwt

【分析】

这里希望建立的图像是让自转轴倾斜，而太阳光水平直射。因此，要从太阳光直射纬度位置去思考北极点所在的位置。如下图，当太阳直射的纬度为 sunangle ，且直射点定为 (1,0,0)，此时就可决定北极点的位置为 (sin(sunangles), 0, cos(sunangles)) 。

【操作】

主要先建立球面，再利用滑动条 sunAngle 来设定北极点于自转轴的位置。

O = (0,0,0)

eq1 : x^2+y^2+z^2= 1 #射定球面

#滑动条调整入射角为 -25.5 到 23.5

sunAngle= 滑动条(-23.5deg,23.5deg,0.1deg,1,100)

# 北极点

N = ( sin(sunAngle),0, cos(sunAngle))

#自转轴

lon: 直线(O,N)

b: x = 0

任务二：纬线的制作

【目的】建立球面上的赤道、纬线。

参考视频：https://www.bilibili.com/video/BV1u4411P79R?p=4

GGB：https://www.geogebra.org/m/rpvq55df#material/dcpgr5wf

【思路】什么是纬线？其实就是平行与赤道面的圆。因此，要绘制纬线就先建立与赤道面平行的面，并求这些面与球面的相交曲线。

【操作】

1. 建立赤道：赤道面为垂直自转轴 lon ，过球心 O 的平面，可用【垂直平面(O,lon)】建立赤道面，接着用【相交路径】来取得平面与球面的相交曲线，可将这两个指令复合为一行，参考如下。

c = 相交路径[垂直平面(O, lon), eq1]

# 其中 eq1 为球面的变数名称

2. 建立纬线：过纬线与球面相交的平面仍是垂直于自转轴 lon ，但差别在于通过的点要随着纬度而变，北纬 23.5° 的纬线要通过点 N*sin(23.5°) ，而北極圈就是要通过 N*sin(66.5°) 的圆。

# 北纬 23.5°

N235 = 相交路径( 垂直平面( N*sin(23.5°),lon), eq1)

# 北极圈 66.5°

N665=相交路径( 垂直平面( N*sin(66.5°),lon), eq1)

# 南回归线

S235=相交路径( 垂直平面( N*sin(-23.5°),lon), eq1)

# 北极圈 66.5°

S665=相交路径( 垂直平面( N*sin(-66.5°),lon), eq1)

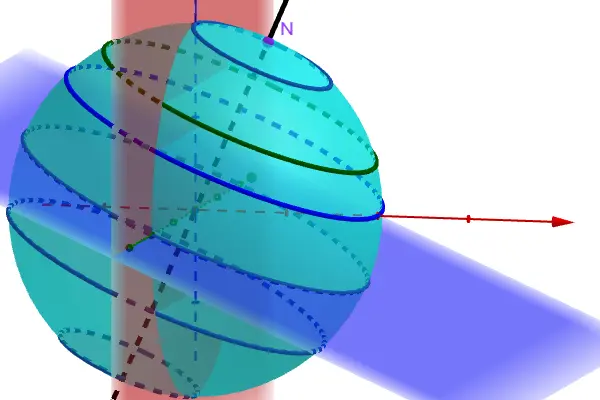
3. 建立动态的纬线：先建立滑动条 latitude = 45° 范围从 -90° 到 90° 。再建立过 N*sin(latitude) 垂直于自转轴的平面，再取得与球面的交线。

latitude = 滑动条(-90deg, 90deg, 0.1deg,1,100)

h = 相交路径( 垂直平面( N*sin(latitude) ,lon), eq1)

## 注意 eq1 为球面方程

任务三：纬线上的动点

【目的】建立球面上的赤道、纬线。

参考视频：https://www.bilibili.com/video/BV1u4411P79R?p=5

GGB：https://www.geogebra.org/m/rpvq55df#material/dcpgr5wf

【思路】一般处理单位圆上的动点可以利用 ( cos(t), sin(t) ) 来表示。这个也可视为 cos(t)*(1,0) + sin(t)*(0,1) 。而现在要实现纬线上小圆的动点就可借用这概念，建立一个坐标系，取得这个坐标系上的两轴方向 vpx， vpy 方向。这时动点就可表示 cos(t)*vpx + sin(t)*vpy ，用此来实现动点。

【操作】

1. 建立阳光的阳光射线：主要利用【射线】来建立，需要个定位起点，方向为 (1,0,0)。

# 建立直射点 S

S=(1,0,0)

# 建立阳光直射的线

sunline = 射线(S,S+(1,0,0))

2. 找出四个定位点：为了处理这个纬线上的坐标系，先建立新坐标系上的 4 个点 (1,0), (-1,0), (0,1), (0,-1)。

# 先建立新坐标系的 (1,0), (-1,0)

交点(平面(O,S,N), h )

## h 是随滑动条移动的纬线,

## 平面(O,S,N) 是过北极垂直赤道的平面

## 这个指令会取得两点，再将其命名为 PX00, PX12

# 再建立(0,1) , (0,-1)

交点(垂直平面(N, 向量(PX1,PX2)) , h),

## 这个指令会取得两点，再将其命名为 PY06, PY18

3. 建立动点：这是此节的重点，要建立圆周运动的动点，就要建立一个坐标轴，接着才能利用 cos， sin 搭配新的坐标轴来绘制此圆的动点。

# Pl 为纬度 latitude 的纬线圆心，位在对称轴上

Pl = O + 向量(O,N)* sin(latitude)

# 为了建立纬线上的动点，需要建立此圆上的坐标轴 vpx, vpy

vpx = 向量(Pl,PX00)

vpy = 向量(Pl,PY06)

time = 滑动条(0,24,1,1,100)

Pt = Pl + cos(time/24*2*pi)* vpx + sin(time/24*2*pi) *vpy