期望O(nlogn)的最长公共子序列，Hunt-Szymanski算法的论文和复现

事先说明，这个算法你大概率在竞赛环境用不到。因为竞赛环境的数据都是构造出来的最坏数据。这个算法在这种数据下的表现可以被卡到O(nmlog(n))，空间O(nm)。并且构造这种数据很容易，令str1="AAAAA"，str2="AAAAAAA"即可。

但是相对的，它在两个序列的元素值域比较大，匹配数比较少的情况下会非常有效。

本文假设你已经学过了最长公共子序列以及其经典的n*m的dp做法，后文提到的所有LCS是Longest Common Subsequence的缩写。

背景（废话）

小组里给了个语料对齐的任务，用实际的例子来说，可以看这个链接：https://wiki.mnbvc.org/doku.php/%E5%AF%B9%E9%BD%90%E7%AE%97%E6%B3%95#%E5%9F%BA%E4%BA%8E%E6%9C%80%E9%95%BF%E5%85%AC%E5%85%B1%E5%AD%90%E5%BA%8F%E5%88%97

方案用了一个最长公共子序列，调的是pylcs这个库，里面的C++实现用了两个n * m的int数组，于是我们的程序在跑长达1MB的大文件时不出意外的炸内存了= =

炸内存还不是主要的问题，稍微魔改了一下，优化到只用1/32的内存，虽然现在是能跑了，但是这个文件仍然需要跑15分钟。其实用LCS来做这个问题不是很有效，我本来都想把方案改进一下，但是网上冲浪的时候遇到了这么一个期望nlogn的算法，看了一下觉得还挺高效的，行，哥们不做方案优化了，重拾旧业开始搞算法。

参考资料

https://en.wikipedia.org/wiki/Hunt%E2%80%93Szymanski_algorithm#cite_ref-8 维基的资料

https://codeforces.com/blog/entry/91581 算法基本思想讲解

https://cse.hkust.edu.hk/mjg_lib/bibs/DPSu/DPSu.Files/HuSz77.pdf 论文

https://github.com/sgtlaugh/algovault/blob/0ba0b3eb0d2e31e78de05da188f13d8d7d0365ae/code_library/hunt_szymanski.cpp 一个短小精悍的C++实现，但是只能求长度，直接用它的下标数组生成LCS是不对的

https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=1460&context=cstech 这个是下界改进，和本文无关，我还没看

思想

如果我们需要求LCS的两个序列比较随机，或者说它们的匹配比较稀疏，这样我们在算LCS的时候，可以从匹配出发，而不需要算一个n*m的dp。举个例子，我们有acbdd和cabad两个序列，把它们画成一个匹配矩阵就是这样：

如图，蓝色格子表示匹配上的元素。我们可以只关心图中的蓝色格子。

算蓝格子很简单，随便用一个桶数组或者哈希表就能实现。

现在，我们的LCS问题可以在图中转化成一个非常形象的问题：寻找一个蓝格子表，使得其横坐标在图中严格递增，同时纵坐标严格递减。

（是不是有点像二维偏序的味道？）

于是几何佬半途抢过键盘开始动手了：我先扫描线从左到右搞一下横坐标，然后我用一个std::set这样的有序容器维护一下纵坐标就做完了。

我知道你很急，但是我们先别急。首先，我们会做最长上升子序列，O(nlogn)做完，一个数组二分插入贪心完事。然后，如果我们把这个图稍微变一下……

由于我们按列展开了这个表，每列最多只有一个元素，然后现在我让你从左到右横着扫一遍，让你求一个最长严格下降子序列，是不是会做了？

为什么是倒序枚举？因为我们不希望一个匹配被计入答案多次，因为正序枚举会计入。感性理解一下。

然后就剩最后一个问题了，我们把它倒序枚举之后，就不能恢复原来的匹配串了。

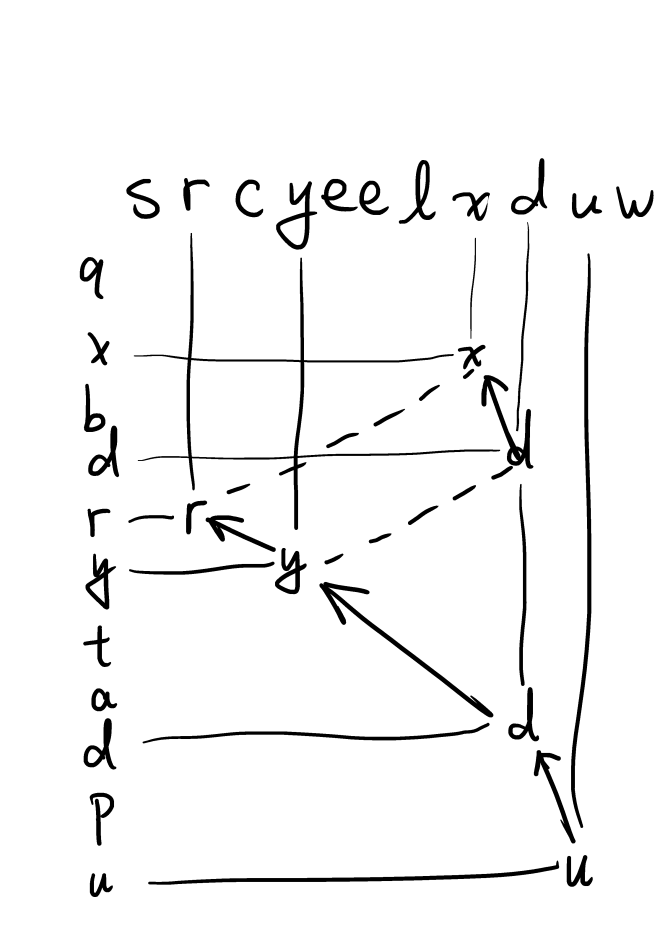
如图，我们从左到右扫描srcyeelxduw的时候，我们希望得到的LCS应该是rydu，但是由于我们拿一个数组记LIS，在更新的时候这个数组是这么变的：

{0: r}

{0: r, 1: y}

{0: x, 1: y}

{0: x, 1: y, 2: d}

{0: x, 1: d, 2: d}

{0: x, 1: d, 2: d, 3: u}

虽然最后LCS的长度是算对了，但是因为我们目前没记它上一次连接的是哪个字符，所以我们最后没有办法恢复原来的LCS。

如果需要这个LCS怎么办呢？我们得引入一个前向链表，这个链表占用的空间是图中的蓝格子总数。所以当匹配数被构造满的时候，这个表的大小还是O(nm)的。

废话说够了，可以上代码了

实现代码

https://github.com/voidf/pylcs/blob/master/src/main.cpp#L65 本人魔改的pylcs，你可以很容易的把核心逻辑抽出来拿去交题