2023 知识论 2023.03.15 柏拉图的知识论（III）

The Theaetetus account 泰拉泰德篇

• “Knowledge is perception”
• Motivation
• perceptual K 常见
• 人是万物的尺度 人感受事物为真或为假
• 是一种对“同一个问题”的不同意见的解释——relativism 相对主义
• Objections
• K cares about Truth
• Self-defeating 相对主义的说法也要被自身的主张质疑
• Meta-relativism
• 非 perceptual K 的存在：
• 数学知识
• epistemic perception 和 raw perception（原初感觉）
• The wind is cold ＆ the wind is cold for me
• 我们能区分A 和 it seems like A
• “Knowledge just is a true judgment or true belief”
• False belief 是可能的吗？
• In Plato's theory, to have what is not in mind是不可能的

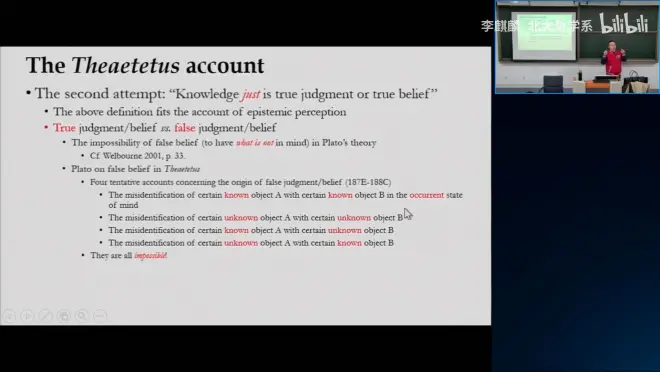
• Wax metaphor 蜡烛比喻
• Aviary metaphor 鸟笼比喻
• Possessing knowledge and having K 拥有一个知识 和 当下有一个认知状态 的区别
• 延伸问题：K is teachable/learnable/acquirable?
• Compare: Recollection 知识回忆说
• Objections
• 雄辩的律师 用persuading 的方式给了听众True Belief，但没有用teaching的方式，你和看到现场的证人是认知上是不同的。
• 认知通路不合法
• “Knowledge is true judgment with Logos/an account”
• Clarification of Logos/Account
• 不是简单的说出信念
• 不是把部分都说出来
• 不是说出那些有标记性的东西
• 但Plato没有对Logos/Account给出正面的定义
• 两个策略
• JTB 的路径
• 知识 和 其他相似概念的对比和区别

Gettier Problem

• The Context of Gettier's Problem
• History
• Two presuppositions
• False belief can be justified （J和T可以分离）
• 传递性：对于命题P， P蕴含Q，如果S相信并证成P，那么S相信并证成Q.

• Two counter-example

Epistemic Closure

• Alternative Theory
• P和Q相互替代（语境不敏感）
• The background of Closure
• Mathematical concept of closure 封闭性的数学定义
• 某个集合进行某个操作是封闭的，当且仅当，所有的元素进行该操作，得到的输出也在该集合中。
• 太严格了，不适合刻画知识论
• Closure under logical implication（CLI）

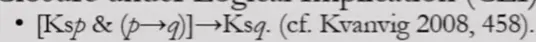
• Epistemic Closure Schema(ECS)
• 解释了S和蕴含式之间的认知关系

• Closure under Known Implication(CKI)
• 问题：如果主体从来没把p 和 p蕴含q 联系起来考虑，那在事实上主体也不知道q

• Antecedent-strengthen CKI 前件增强版
• 为了解决上面的问题，引入了K以外的操作，在数学上并不是完全的封闭

• Consequent-weakened CKI（CKI-CW）后件削弱版
• 用于削弱的算子[[K]]： in a position to know

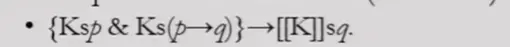
• DeRose's Argument from Ignorance
• 为什么知识论关心封闭原则
• The Argument from Ignorance 一个怀疑论的论证
• I do not know that not-H(比如我不知道我是不是缸中之脑）
• If I do not know not-H, then I do not know that O(O是一个常识命题）
• So, I do not know that O
• 这样的论证是依赖于封闭原则的
• 一定要接受封闭原则吗？
• Dretske on the failure of closure
• 一些知识命题是不满足封闭原则——斑马和伪装的很好的骡子
• evidential relation
• Nozick on the failure of closure
• 封闭原则和反事实条件句
• 反事实条件句要给可能世界排序，找到与本世界最近的相似世界
• 某些可能世界我们的认知强度是达不到的——可错主义直觉
• 非P的可能世界更容易使得封闭原则失效
• 反事实的敏感性和安全性（？）
• Warfield‘s diagnosis