俯瞰式学习·深刻理解线性代数·上篇(深刻≠掌握)
没有谁能拒绝降维打击式的学习。如何巧妙地设置俯瞰,就像杰出的指挥官一样部署火力,必将在新一代教学方案上塑造传奇。
上篇的行文主线是解线性方程组,具体节点是:
鸡兔同笼→克莱姆法则→行列式→行列式=0→;
克莱姆法则→解的意义→高斯消元法→线性变换→

线性代数在解线性方程组的运算实践中,发展出来了矩阵和线性变换的相关理论。
一个经典的解线性方程组问题:鸡兔同笼。

有一种做法是先假设全是鸡或者假设全是兔:

这种解法是克莱姆法则的一个特例。它的思想在几何直观上是卓越的:同底不等高的面积之比=高的比

对于这个算术问题:
在这种写法里,一维的数表被称为“向量”,二维的数表被称为“矩阵”,矩阵将向量进行变换。
全是鸡或兔的做法在图2中的公式与套用克莱姆法则公式是一致的(如图4),图2中的公式只不过是在行列式(2维数表加竖线)计算时有一行的元素都是1,恰好计算省事了:

如果数表中的系数不为1时,行列式是怎样计算的?
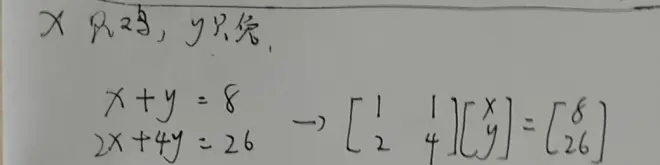
比如我们给出这样一个线性方程组:

我们将x和y视为一种“向量的伸缩率”,是一种勾兑矩阵中两个列向量的比例。
我们现在将这两个列向量当作基底,将它在坐标系中画出来:

我们可以直观清晰地看到:线性方程组就是一个分向量的合成过程,而解线性方程组则是合向量的分解过程。
人们发现了这样一种平行四边形:

这种平行四边形在变换前后是同底不等高的,则面积之比即为伸缩率。如图,y=蓝色平行四形面积/粉色平行四边面积=2;

同理,对于另一个伸缩率x,


2维的行列式就是这种手性的平行四边形面积。3维时是对应的平行六面体体积。行列式就是这种向量们围成的手性体积大小。我们都是用的右手系,所以右手性为正、左手性为负。
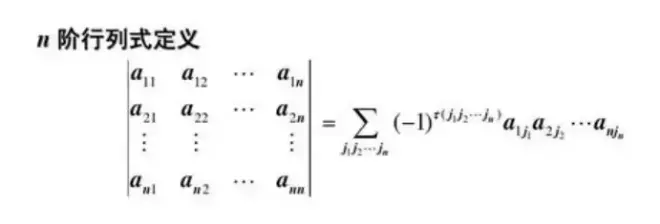
这里的τ表示“逆序数”,这个“逆序”是相对“正序”而言,逆序一次相当于镜像一次,改变手性,逆序两次镜像两次,手性不变。

镜像可以让左右手彼此完成一次翻转。

至此,我们借助生动的几何图景,获得了两个高屋建瓴的俯瞰:
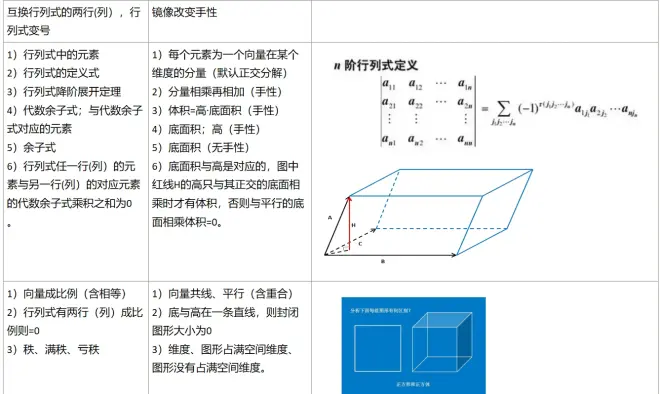
一是行列式的几何意义:以向量作为封闭图形的边长、按平行四边形法则张成的封闭图形的手性大小。
二是克莱姆法则的几何意义:以解向量为系数矩阵中列向量的伸缩率,并用同底不等高的平行四边形面积之比来算出。
在知识学习中,获得俯瞰是极为重要的,有助于使思维清晰。

一些生硬的知识在拥有俯瞰后一目了然:

这些定理在几何上都是显然的:
行列式在有些情况下=0,其几何解释为封闭图形中有向量“被投影”。比如说下图中向量组{a,b,c}张成的平行六面体是三维的,但向量组{AD,b,c}张成的封闭图形就是底面的平行四边形。相当于有高度的向量a被投影到{b,c}所在平面。

向量组如果亏秩,就是线性相关的,即向量组中有向量可以被其他向量“勾兑”。

VA的三个向量共面时,向量个数大于当前向量组所占空间维度,即亏秩,一定有向量可以被勾兑出来,比如V2可以被V1和V3勾兑出来。这种勾兑我们称为“线性表出或线性表示”。
向量组中那些不能被相互勾兑的向量们,称为线性无关的向量组,简称无关组,比如上图中的VB。当包含向量个数最多的时候,我们称之为“极大无关组”。它在几何上也是显然的,就是挑那些向量可以围成维度与向量个数相同的封闭图形。比如VA中任选两个向量即可。如果一个3阶的向量组只能围成2维的封闭图形,则其极大无关组就包含2个线性无关的向量。

你现在已经初步尝到了获得俯瞰后的甜头。而作者本篇文章的特色也在于如何巧妙地设置俯瞰,打一个生动的比方,它们就像是巩固我们知识版图的长城哨所(立于岭上):

知识的版图并不总是一马平川的。我们熟知的思维导图是河流状的,它在“思维的平野上”是奏效的,比如一些识记类的知识。而有认知难度的“思维的山川”会导致最具总结性的干流往往是在学完后才能出现,初学者往往困惑于半山腰的云雾中。

具有“分水岭”地位的公理们,有时候会难以攀登。这就需要教学者“修筑某些栈道工事”,有时候可以在公理系统的地貌之上人为修筑一些俯瞰。比如这篇文章的几何观点及克莱姆法则的几何意义。
一门学科的图景,可能有像蓝天白云一样的宏大叙事或背景,但最关键的是拿下这片山地并驯服河流,使之灌溉大片的领域来生产庄稼和各类果实。

《高观点下的初等数学》的作者、一代数学教学宗师克莱因认为,教师掌握的知识要比他所教的多得多,才能引导学生绕过悬岩、渡过险滩。所以与人民利益一致的教员同志会尽可能让群众容易地登顶造化钟神秀的俯瞰,绝不会故弄玄虚或引入歧途。
克莱姆法则与行列式的几何图景是线性代数的第一险要关口,它也是通往后续章节的门户。主路线仍是解线性方程组,从解线性方程中来,到解线性方程组中去。沿着这条蜿蜒于山岭间的主路,前往下一个关口:高斯消元法。

在克莱姆法则中,如果分母位置上的系数矩阵的行列式=0,则解会成为无穷大——然而事实上也确实是“无穷大”——无穷多的点!我们先来看线性方程组的解对应只有一个点(唯一解)的情况:回顾刚才图5的线性方程组:

我们知道二元一次线性方程的几何意义是坐标系中的一条直线:

二元线性方程组的几何意义就是联立直线们,则解就是直线们的交集。
三维时,三元一次线性方程的几何意义是比3维空间小一维的2维平面。此时求方程组的解就是求平面的交线。

推广到n维,n元一次方程的几何意义就是n-1维的超平面。求解就是求交集。而之所以是n-1维,是因为n元一次方程的系数向量消灭了一个自由度的不确定性,使自变量们被约束在n-1维的超平面内活动。
上图中的方程组的得数向量均为0,如果系数向量和解向量的内积=0——则说明这两个向量正交。如果一个系数矩阵左乘一个解向量=零向量,则这个矩阵和解向量在空间上是正交的,此时的几何图景是“旗杆竖地”:

可以简明地展示:系数矩阵的维度+解空间的维度=n。这也是齐次线性方程组的一个重要定理。
我们学的矩阵的相关知识,有一大部分都是应用于解线性方程组。对于矩阵,最重要的知识莫过于初等行变换。初等行变换经常运用于高斯消元法,我们总是习惯于用消元法来解方程的,如下图:

它的几何解释是:尽可能使直线方程“摆正方向”,即由倾斜变换到横平竖直。

上图的系数矩阵被称为“行阶梯形矩阵”,它不是消元彻底的系数矩阵,消元彻底的系数矩阵我们称为“行最简形矩阵”,
它的几何解释是直线方程完全与坐标轴平齐或垂直,则解集一目了然

即上述线性方程组的有唯一解(2,2)。
上述两元一次方程组的高斯消元法,其实是对系数矩阵进行初等行变换。一共有三种初等行变换,它们分别是互换两行、数乘、数乘再相加到某一行,它们在几何上的解释分别为:直线编号改变、直线的法向量伸缩、直线系(一种绕定点旋转直线的操作),都不会改变直线组的交点(解)。
对系数矩阵进行初等行变换这一操作也可以用矩阵来描述,用初等行变换矩阵。比如对第2行向量×3再-第一行向量,可以这样描述:

如上图,我们在原来的系数矩阵左侧乘以具备这一功能的矩阵。我们对矩阵这个静态的2维数表有了更深入的认识:矩阵是描述线性变换的向量组。而且当变换矩阵在左侧时是行变换。回顾克莱姆法则,解向量作为将系数矩阵列向量进行列变换的伸缩率,事实上向量本身也是一维的矩阵,变换矩阵在右侧时是列变换。
至此,高斯消元法在知识版图中的地缘意义凸显:高斯消元法是登顶线性代数最高俯瞰点——线性变换观点的另一个门户(上一个门户是克莱姆法则)。

线性变换观点是top级俯瞰。我们首先用它来解决一个初学者常见的困惑:在求解线性方程组时,为什么只能对系数矩阵进行行变换而不能进行列变换?因为列变换是在更改解向量:

此时的得数向量是在默认的标准单位正交基下的坐标:
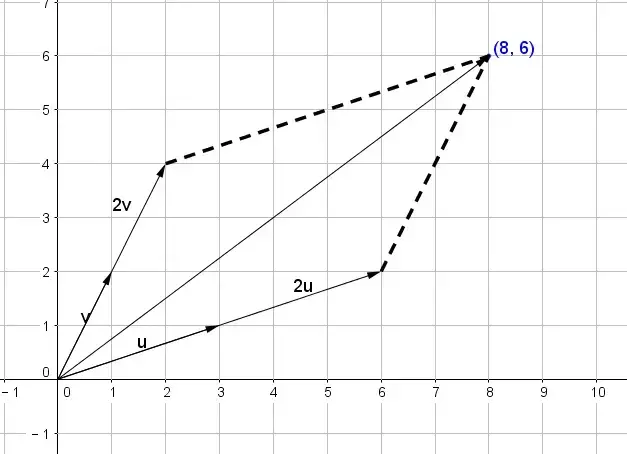
如果对系数矩阵的两个列向量u和v变换,无论是伸缩、互换位置还是伸缩+旋转,则这个得数向量就不再是现在坐标系中的2u+2v了,也就是说方程的解不再是(2,2),这样一来就“算错了数”。

下一篇是在top级俯瞰线性变换观点下重新审视线性代数,将比这一篇还要传神,敬请期待。

