2.8 路径积分量子化（二）

对于电磁场的路径积分量子化我们要考虑它的规范不变性。

一种解决方法是限制积分的区域在一个超曲面上，而不是整个空间。如此一个超曲面的方程为：

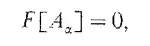
我们将其带入到电磁场路径积分量子化的定义式中。并且为了确保规范不变性。这两个临近的超曲面的关系为：

当\Lambda=0时，表示同一个超曲面。其中M是依赖于规范的选择的。例如，在Landau规范中

并且有

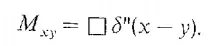
这个是方便的定义：

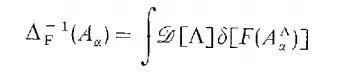
我们可以从中看到规范不变性。当我们利用超曲面积分时，两个超曲面之间的积分公式中右边的第一项消失。上式中的积分可以被计算，改变积分变量为M\Lambda：

经过一系列积分变量变换和积分，我们可以得到：

然后我们注意一些积分无关的项，定义：

注意在这个过程中积分范围的变化，可以确保我们使用超曲面的结果。

限制积分再超曲面的方法不仅仅只有这一种。后续的方式可以参见书中的内容。

在本节的最后，我们简要谈谈路径积分 (2.115) 的收敛性。一般来说，由于作用 S 是实数，积分中的指数是纯虚的。因此，对整个函数空间进行积分时，积分的定义通常是不正确的。在前面的章节中，我们通过谨慎使用无穷小因子改善了这一问题。正如第 2.7 节所述，使用  定义费曼格林函数等同于传递虚时间描述，其中场是在欧几里得空间而不是闵科夫斯基空间定义的。如果时间有序场积的真空期望值（如 (2.117)）在复¢平面上是解析的，那么我们就可以在欧几里得空间构造一个场量子化，其中，路径积分采用定义明确、收敛性强的高斯形式（至少对于多种拉格朗日量而言），最后通过从路径积分 "旋转 "回时间t来恢复闵科夫斯基空间理论。这种技术在实践中经常使用。然而，当进入弯曲时空时，可能会出现没有 "欧几里得化"时空与原来的伪黎曼时空相对应。