电弧焊接增材相关物理基础理论介绍(三)

1.2.2 动量方程
纳维-斯托克斯方程,又称为粘性流体动量平衡方程。
流入和流出系统的动量差值+其他力对系统作用的总和=系统动量的变化量。力包括表面力和体积力。对于黏性流体,动量的传输有两种基本形式:流体质量对流基础上进行的对流传输;流体的黏性引起的动量传输。物理意义:理想流体微分方程表达了作用在单位质量流体上的力与流体运动加速度之间的关系,是流体动力学的基本方程,对于不可压缩和可压缩的流体均适用,也适用于所有的理想流体的运动。物质导数的物理意义为:它是运动的流体微团的物理量随时间的变化率,它等于该物理量由当地时间变化所引起的变化率与由流体对流引起的变化率的和。随流体运动的流体微元的瞬时变化率=由当地时间变化引起的变化率+由空间运动引起的变化率。
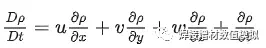



此外,也可以通过数学中的链式法则来推导得到,由于密度是空间和时间的函数,则根据链式法则:

动量方程又分为守恒形式和不守恒形式两种。


表面力和体积力



其他资料推导过程:
(1)非守恒方程
根据牛顿第二定律可以得出:F=ma;
因此:对于流体微元:方程式的左边:F=表面力+体积力
方程式的右边,当仅考虑x方向的作用力时:

回到方程式的左边,体积力可以表示为:
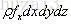
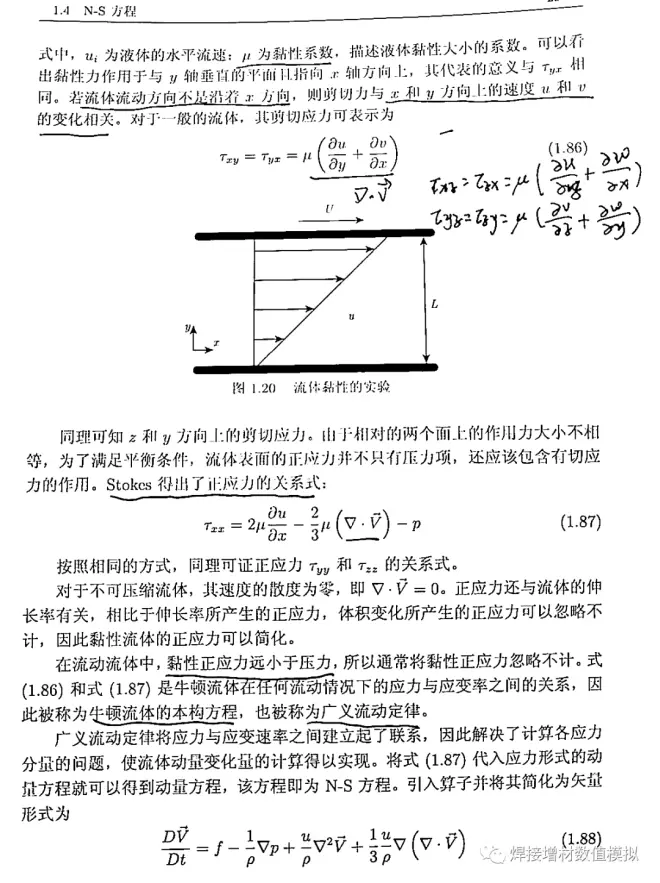
表面力可以表示为流体微元在x方向所有正应力和切应力之和,其表达式如下所示:

整理可得:

将体积力表达式、表面力表达式和方程右边表达式代入牛顿第二定律表达式中可得:

化简可得:
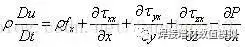
同理可得y方向和z方向的两个方程:


(2)守恒方程
以x方向为例:
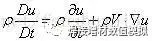
根据:
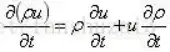
可得:

将该式子带入上式子:
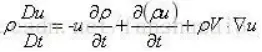
根据标量与向量的乘积的散度的向量恒等式:




将该式子带入非守恒动量方程表达式得:
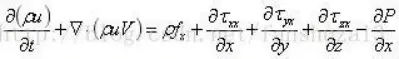
所谓守恒形式和非守恒形式的区别如下:
如果方程可以写成控制方程通用形式:

,即其对流项均采用散度形式表示的形式,这种控制方程的形式称为控制方程的守恒形式,这种方程称为守恒型的控制方程。从微元体的角度考虑,守恒型控制方程等价于非守恒型控制方程,但是在计算一些特殊流场时,守恒型方程和非守恒型控制方程有较大的区别。根据《数值传热学》的描述,在计算激波时,守恒型方程计算结果光滑而稳定,而非守恒型控制方程会引起数值计算结果的震荡,造成错误。并且只有守恒型控制方程才能在计算有限大小控制容积内部所研究的物理量时守恒定律仍然得到满足。(总结自陶文铨《数值传热学》(第二版))
————————————————
参考:
1. https://blog.csdn.net/fanshuzai3/article/details/79190769
2. 樊丁,黄健康《弧焊物理过程建模与数值分析》

