杂货铺科学（210712b）：玩蹦蹦床的小水滴。

我是小水滴，我在玩蹦床，你在哪？

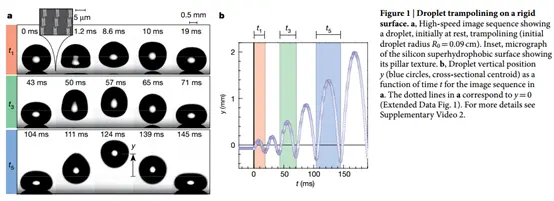
普通水滴掉地上不但没有粉身碎骨，反而越弹越高！？最新一期的Nature文章（doi:10.1038/nature15738）再次挑战我们的直觉。

揭秘：

1、小水滴的妈妈在杂货铺给他买了张蹦床（图a插画），这张蹦床能保护小水滴不被摔坏。

2、小水滴玩之前黄豆吃得不少，每次触床那会儿就忍不住要……

题目Spontaneous droplet trampolining on rigid superhydrophobic surfaces
作者Thomas m. Schutzius1*, Stefan Jung1*, Tanmoy maitra1, Gustav Graeber1, moritz Köhme1 & Dimos Poulikakos1
摘要Spontaneous removal of condensed matter from surfaces is
exploited in nature and in a broad range of technologies to achieve
self-cleaning1,2, anti-icing3–6 and condensation control7,8. But
despite much progress5–7,9–14, our understanding of the phenomena leading to such behaviour remains incomplete, which makes
it challenging to rationally design surfaces that benefit from its
manifestation15–18. Here we show that water droplets resting on
superhydrophobic textured surfaces in a low-pressure environment
can self-remove through sudden spontaneous levitation and subsequent trampoline-like bouncing behaviour, in which sequential
collisions with the surface accelerate the droplets. These collisions
have restitution coefficients (ratios of relative speeds after and
before collision) greater than unity19 despite complete rigidity of
the surface, and thus seemingly violate the second law of thermodynamics. However, these restitution coefficients result from an
overpressure beneath the droplet produced by fast droplet vaporization while substrate adhesion and surface texture restrict vapour
flow. We also show that the high vaporization rates experienced
by the droplets and the associated cooling can result in freezing
from a supercooled state20,21 that triggers a sudden increase in
vaporization, which in turn boosts the levitation process. This
effect can spontaneously remove surface icing by lifting away
icy drops the moment they freeze. Although these observations
are relevant only to systems in a low-pressure environment, they
show how surface texturing can produce droplet–surface interactions that prohibit liquid and freezing water-droplet retention
on surfaces.