郑涛（Tao Steven Zheng）著

【问题】

证实正态分布（normal distribution）

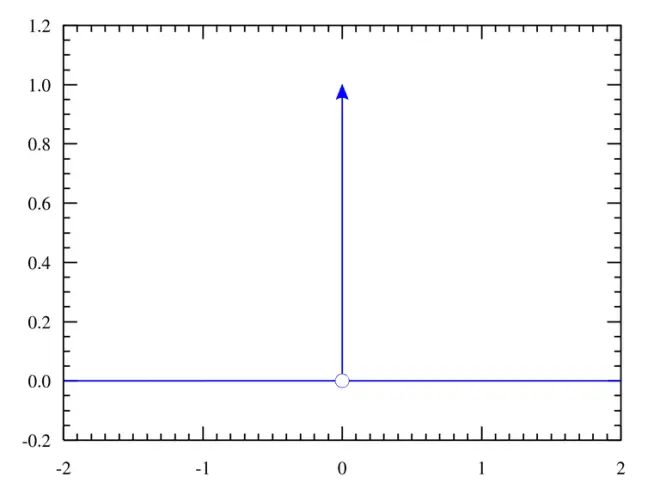
满足热传导方程（heat equation）[1] （ 是常数， ）， 以初始条件为 ，其中 是 狄拉克δ函数（Dirac delta function）[2]。

[1] 热传导方程（heat equation） 相等于 。

[2] 狄拉克δ函数（Dirac delta function）定义为 。

【题解】

求 对于 的一阶偏导数 （first partial derivative）：

求 对于 的一阶偏导数 （first partial derivative）:

求 对于 的二阶偏导数 （second partial derivative）：

因此，

热传导方程 两侧是相等的！

狄拉克δ函数实际上是一个分布（distribution），而不是一个函数（分布可以说是比较广义的函数）。事实上，该分布可以用极限来定义

所以，狄拉克δ函数（Dirac delta function）自动满足初始条件 。