Electromagnetism||Electrostatics

2021-01-18 10:09 作者:湮灭的末影狐 0人读过 | 我要投稿

//I'm here in Nankai University.

//And next term we will have an Italian professor... to teach Electromagnetism.

//And obviously it will be completely taught in English.

//So I write this note, simply to practice English...so I won't be overwhelmed...

//Let's start it.

1. Electrostatics: charges and fields

1.1 Electric charge

All charged particles can be divided into two classes. Two charges of the same class repel each other, while two charges of different classes attract each other. (By contrast, there's only one kind of gravitational mass, so every mass attract every other mass.)

This is a fundamental property of an electric charge, sign of the charge: positive or negative.

For every kind of particle in nature there can exist an antiparticle carrying charge of the opposite sign, with exactly the same mass. When a particle meets its antiparticle, they annihilate and produce energy. For example, an electron's charge is negative; its antiparticle called positron has a positive charge.

1.2 Conservation

Electric charge has an essential property that:

The total charge in an isolated system never changes.

This is called the conservation of charge. This law can be written in different forms:

$%5Csum_%7B%5Crm%20in%7DQ_i%20%3D%20%5Crm%20Const$

$%5CDelta%20Q%20%3DQ_%7B%5Crm%20in%7D-Q_%7B%5Crm%20out%7D$

or we can associate this law with electric current:

$%5Ciint_S%20%5Cvec%7Bj%7D%20%5Ccdot%20%5Cmathrm%7Bd%7D%20%5Cvec%7BS%7D%3D-%5Cfrac%7B%5Cmathrm%7Bd%7D%20Q%7D%7B%5Cmathrm%7B~d%7D%20t%7D$

where Q is the total charge inside the surface S. We also have differential form:

$%5Cnabla%20%5Ccdot%20%5Cvec%20j%20%2B%20%5Cfrac%7B%5Cpartial%20%5Crho%7D%7B%5Cpartial%20t%7D%3D0$

1.3 Quantization of charge

The electric charges we find in nature come in units of one magnitude only, equal to the amont of charge carried by a single electron. We denote its magnitude by $e$ .

But there is internal structure of all the strongly interacting particles called hadrons, including protons and neutrons. The internal structure involves basic units called quarks, with charge $2e%2F3$ or $-e%2F3$ .

1.4 Coulomb's law

Coulomb's law describes the interaction between two point electric charges at rest:

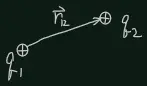
$%5Cvec%20F_%7B12%7D%20%3D%20k%20%5Cfrac%7Bq_1%20q_2%7D%7Br_%7B12%7D%5E2%7D%20%5Chat%20r_%7B12%7D$

Also the force obeys Newton's 3rd law:

$%5Cvec%20F_%7B12%7D%3D-%5Cvec%20F_%7B21%7D$

$k%3D8.988%20%5Ctimes%2010%5E9%20%5Crm%20N%20%5Ccdot%20m%20%5Ccdot%20C%5E%7B-2%7D$ is a constant, and for historical reason,

$k%3D%20%5Cfrac1%7B4%5Cpi%20%5Cepsilon_0%7D$

where $%5Cepsilon_0$ is called vacuum dielectric constant.

1.5 Energy of a system of charges

According to Coulomb's law, we know electrical forces are conservative, so we introduce a useful concept, energy. Consider two charged particals with charge $q_1%2Cq_2$ respectively are brought together from very far, and the ultimate distance between them is r, How much work must be done?

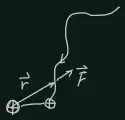
$W%3D%20%5Cint%20_%5Cinfty%20%5Er%20-%20%5Cfrac%7Bq_1%20q_2%7D%7B4%5Cpi%20%5Cepsilon_0%20r%5E2%7D%5Cmathrm%20d%20r%3D%20%20%5Cfrac%7Bq_1%20q_2%7D%7B4%5Cpi%20%5Cepsilon_0%20r%7D$

So the energy between these two particles is equal to W. This work is the same whatever the path of approach. For a system with N particles, total electrostatic energy is

$U%3D%20%5Cfrac12%20%5Csum_%7Bj%3D1%7D%5EN%20%5Csum_%7Bk%20%5Cneq%20j%7D%5Cfrac%7Bq_jq_k%7D%7B4%5Cpi%20%5Cepsilon_0%20r_%7Bjk%7D%7D$

Or we can write

$U%3D%5Ciiint%20%5Cfrac12%5Crho%20%5Cphi%5C%2C%20%5Cmathrm%20d%20V$

Where $%5Cphi%20$ is the electric potential, what we are going to introduce in chapter 2.

1.6 is an example of finding electrical energy in a crystal lattice, so I'll just skip this part.

1.7 Electric field

Suppose there are several charges $q_1%2C%20q_2%2C...%2Cq_n$ , and force on another charge $q_0$ is:

$%5Cvec%20F%20%3D%20%5Csum%20_%20%7Bj%3D1%7D%5En%20%5Cfrac1%7B4%5Cpi%20%5Cepsilon_0%7D%20%5Cfrac%7Bq_0%20q_j%7D%7Br_%7B0j%7D%5E2%7D%20%5Chat%20r_%7B0j%7D$

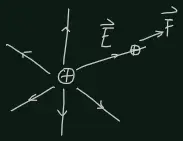
If we define an electric field strength vector:

$%5Cvec%20E%3D%5Cfrac1%7B4%5Cpi%20%5Cepsilon_0%7D%5Csum%20_%20%7Bj%3D1%7D%5En%20%5Cfrac%7B%20q_j%7D%7Br_%7B0j%7D%5E2%7D%20%5Chat%20r_%7B0j%7D$

The force on a charge is then

$%5Cvec%20F%3Dq_0%5Cvec%20E$

We can also consider continuous charge distribution of the source of the electric field,

$%5Cvec%20E%3D%20%5Cfrac1%7B4%5Cpi%5Cepsilon_0%20%7D%5Ciiint%20%5Cfrac%7B%5Crho%20%5Chat%20r%7D%7Br%5E2%7D%5Cmathrm%20d%20V$

1.8 shows an example of continuous charge distribution, I'll skip again.

1.9 Flux

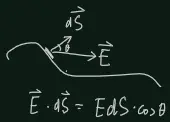
This part introduces the definition of flux of a vector field, which will be useful:

$%5CPhi%20%3D%20%5Ciint_S%20%5Cvec%20E%20%5Ccdot%20%5Cmathrm%20d%20%5Cvec%20S$

is the flux through the surface S.

1.10 Gauss's law

The flux through a closed surface is proportional to total charge inside:

$%5Ciint_S%20%5Cvec%20E%20%5Ccdot%20%5Cmathrm%20d%20%5Cvec%20S%3D%20%5Cfrac%20%7BQ_%7B%5Crm%20in%7D%7D%7B%5Cepsilon_0%7D$

and we have its differential form:

$%5Cnabla%20%5Ccdot%20%5Cvec%20E%3D%5Cfrac%20%5Crho%20%7B%5Cepsilon_0%7D$

$%5Cnabla$ is Hamilton's operator,

$%5Cnabla%20%3D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20x%7D%20%5Cvec%20i%2B%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20y%7D%20%5Cvec%20j%2B%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20z%7D%20%5Cvec%20k$

To prove this law, we can first consider a single point charge $q$ and a surface $S$ . The electric field in the whole space is

$%5Cvec%20E%20%3D%20%5Cfrac%20%7Bq%5Chat%20r%7D%7B4%5Cpi%20%5Cepsilon_0%20r%5E2%7D$

And the flux through the surface is

$%5CPhi%20%3D%20%5Ciint_S%20%5Cvec%20E%20%5Ccdot%20%5Cmathrm%20d%20%5Cvec%20S%20%3D%20%5Cfrac%7Bq%7D%7B4%5Cpi%20%5Cepsilon_0%7D%5Ciint_S%20%20%5Cmathrm%20d%20%5Cvec%20S%20%5Ccdot%20%5Cfrac%7B%5Chat%20r%7D%7Br%5E2%7D%3D%20%5Cfrac%7Bq%7D%7B4%5Cpi%20%5Cepsilon_0%7D%20%5Ciint_S%20%5Cmathrm%20d%20%5COmega$

where $%5COmega%20$ is the total solid angle of surface S. Obviously,

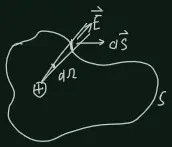
$%5COmega%20%3D%20%5Cleft%20%5C%7B%20%5Cbegin%7Barray%7D%7Bl%7D%0A4%5Cpi%2C%5C%3B%20q%5C%3B%20%5Crm%20inside%20%5C%3BS%5C%5C%0A0%2C%5C%3B%20q%5C%3B%20%5Crm%20outside%20%5C%3BS%0A%5Cend%7Barray%7D%20%5Cright.$

so we have

$%5CPhi%20%3D%20%5Cfrac%20q%7B%5Cepsilon_0%7D%5C%3B%20(q%20%5Crm%20%5C%3B%20inside%5C%3B%20S)$

if there are many particles,

$%5CPhi%20%3D%20%5Ciint_S%20%5Cvec%20E%20%5Ccdot%20%5Cmathrm%20d%20%5Cvec%20S%20%3D%20%5Ciint_S%20%5Csum%5Cvec%20E_i%20%5Ccdot%20%5Cmathrm%20d%20%5Cvec%20S%20%3D%20%5Csum%5Ciint_S%20%5Cvec%20E_i%20%5Ccdot%20%5Cmathrm%20d%20%5Cvec%20S%3D%5Csum_%7B%5Crm%20in%7D%5Cfrac%20%7Bq_i%7D%7B%5Cepsilon_0%7D%2B%20%5Csum_%7B%5Crm%20out%7D0$

therefore,

$%5CPhi%20%3D%20%5Csum%20q_%7B%5Crm%20in%7D%2F%5Cepsilon_0$

1.11~1.14 are examples using Gauss's law, skip again. Here we focus on theoretical points instead of details of calculation.

1.15 Energy associated with the electric field

Suppose we create a spherical shell with total charge $q$ . According to our theory in 1.5, this shell requires energy $U$ to assemble,

$U%3D%20%5Cfrac%7Bq%5E2%7D%7B8%5Cpi%20%5Cepsilon_0%20r%7D$

$%5Cmathrm%20d%20U%20%3D%20-%20%5Cfrac%7Bq%5E2%7D%7B8%5Cpi%20%5Cepsilon_0%20r%5E2%7D%20%5Cmathrm%20d%20r$

And electric field strength near the surface is

$%20E%3D%20%5Cfrac%7Bq%7D%7B4%5Cpi%20%5Cepsilon_0%20r%5E2%7D$

So we can discover that

$%5Cmathrm%20d%20U%20%3D%20%5Cfrac12%20%5Cepsilon_0%20E%5E2%20%5Ccdot%204%5Cpi%20r%5E2%20%5Cmathrm%20d%20r$

$U%3D%20%5Ciiint%20%5Cfrac12%20%5Cepsilon_0%20E%5E2%20%5Cmathrm%20d%20V$

where $w%3D%20%5Cfrac12%20%5Cepsilon_0%20E%5E2$ is called energy density. This is also true for a complicated electrostatic system with different charge distribution in space. The proof is mentioned in Feynman's lecture, and it's quite hard, I'll just skip the proof.

It seems like this energy is "stored" in the field. Our textbook discussed the meaning of this theory...I can't understand and rehearsal well, so let's just see the text: